1よりも小さい数について図で表そうとすれば、「1」を表す正方形を細分割していけばよい。10等分を繰り返してゆくのが10進法であるが、3等分、4等分を繰り返すと、3進法や4進法による小数の表し方となる。ここでは3進法を例として考えてみよう。まず「1」を表す正方形を3等分すると長方形となり、それを更に3等分すると再び小さな正方形ができる・・・。

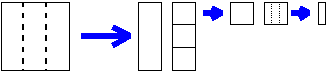
　これらを小1本、小1個、小小1本等と呼ぶことにする。明らかに小1本は1/3を表しているが、これは「1」の正方形を分割していく場合の第1段階の3等分割であるから0.1₍₃₎と表すのである。次に小1個は1/3²であるが、「1」の正方形の第2段階の3等分割として0.01₍₃₎として表す。そして第3段階の3等分割されたものを0.001₍₃₎と表す。これは1/3³を表している。このようにしていくと、一般にＫ進法による小数の表し方が可能となる。そして、0.1_(K)=1/K、0.01_(K)=1/K²、0.001_(K)=1/K³、・・・となる。

　さて次の図は「1」の正方形の拡大図ということにして、斜線部はどのような数を表しているのであろうか。

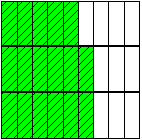
　これは小1本と小1個が2つと小小1本が2つとでできている。従って3進法の小数0.122₍₃₎と表されるが、図より明らかに17/27を意味する。
　0.122₍₃₎=1×1/3＋2×1/3²＋2×1/3³=17/27
として求めることができる。

一般にx=a1×1/K＋a2×1/K2＋a3×1/K3＋・・・＋an×1/Kn＝0.a1a2a3・・・an(K)と表し、小数xのＫ進法表示という。

　では具体的に或る小数や分数を3進法や4進法の小数で表すのにはどうのようにすればよいのか。或る小数xが次のようにＫ進法表示されたとしよう。
　　x=0.a₁a₂a₃・・・a_n・・・_(K)
このような表示は一意的に可能であるから（証明略）このa₁,a₂,a₃・・・が具体的に求められればよいわけである。
x=a₁×1/K＋a₂×1/K²＋a₃×1/K³＋・・・＋a_n×1/Kⁿ・・・ であるから両辺にKをかけると
Kx=a₁＋a₂×1/K＋a₃×1/K²＋・・・＋a_n×1/K^n-1・・・
となるからKxの整数部分がa₁であり、小数部分は
a₂×1/K²＋a₃×1/K³＋・・・＋a_n×1/Kⁿ・・・
と等しいとおける。この方法を繰り返していくと順にa₁,a₂,a₃・・・が求められる。

（例７）10進小数0.609375を4進法表示せよ。

（解） 0.609375=0.a₁,a₂a₃₍₄₎
=a₁×1/4＋a₂×1/4²＋a₃×1/4³＋a₄×1/4⁴・・・
とおく。両辺に4をかけて
2.4375=2+0.4375
=a₁＋a₂×1/4＋a₃×1/4²＋a₄×1/4³・・・
となり,a₁=2,かつ
0.4375
=a₂×1/4＋a₃×1/4²＋a₄×1/4³・・・
となる。以下この方法を繰り返す。
1.75=1+0.75
=a₂＋a₃×1/4＋a₄×1/4²＋a₅×1/4³・・・
より,a₂=1,かつ
0.75
=a₃×1/4＋a₄×1/4²＋a₅×1/4³・・・
3=3+0.000・・・
==a₃＋a₄×1/4＋a₅×1/4²・・・
より,a₃=3,かつ,a₄=a₅=・・・=0
　このようにして
0.609375=0.213₍₄₎となる。

（例８）3/5を3進法で表せ。

（解）3/5=0.a₁a₂a₃・・・₍₃₎
=a₁×1/3＋a₂×1/3²＋a₃×1/3³＋・・・
とおいて両辺に3をかける。
9/5=1+4/5
=a₁＋a₂×1/3＋a₃×1/3²＋a₄×1/3³＋・・・
ゆえにa₁=1,かつ4/5=a₂×1/3＋a₃×1/3²＋a₄×1/3³＋・・・とおいて再び両辺に3をかける。
12/5=2+2/5
=a₂＋a₃×1/3＋a₄×1/3²＋a₅×1/3³・・・
a₂=2,かつ2/5=a₃×1/3＋a₄×1/3²＋a₅×1/3³＋・・・
6/5=1+1/5
=a₃＋a₄×1/3＋a₅×1/3²＋a₆×1/3³・・・
a₃=1,かつ1/5=a₄×1/3＋a₅×1/3²＋a₆×1/3³＋・・・
また両辺に3をかけると
3/5=0+3/5
=a₄＋a₅×1/3＋a₆×1/3²＋a₇×1/3³・・・
ここでa₄=0,かつ3/5=a₅×1/3＋a₆×1/3²＋a₇×1/3³＋・・・
となるが、これは初めの式と同型である。従って計算は今までの過程が繰り返されるだけである。ゆえに3/5=0.12101210・・・₍₃₎となり3進法の循環無限小数になるのでこれを0.1210₍₃₎と書くことにする。

（例７）、（例８）で特徴的なことは、x=0.a₁a₂a₃・・・₍₃₎とおいて両辺に3をかけて、左辺の数の整数部分がa₁、小数部分が0.a₂a₃a₄・・・₍₃₎となり、次にこの小数部分の式の両辺に3をかけてa₂を求めるというように同じような計算を繰り返してゆく。つまり整数部分をより出し、小数部分（分数の場合は真分数）には3をかけてゆくという一種のアルゴリズムである。従って次のような簡便計算が可能となることは明らかであろう。

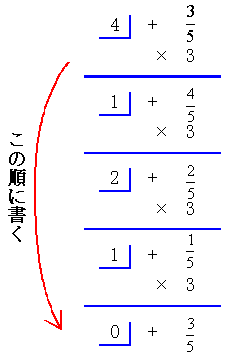
　この計算の矢線の順に書いて、1,2,1,0を求め、以下同じ計算が繰り返されることもわかる。
　また、3/5=3÷5=10₍₃₎÷12₍₃₎と考えて3進法の除法でも求めれられよう。

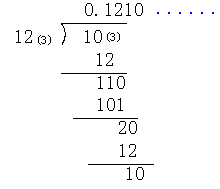
（例９）αは0＜α＜1を満たす実数とする。任意の自然数nに対して,2n-1αの整数部分をanとし、2n-1α=an+bnとおくと、nが奇数のとき0≦bn＜0.5、nが偶数の時0.5＜bn＜1となるという。an及びαを求めよ。（東工大）

（解）題意は2倍、2倍して行くと小数部分が交互に0.5より大、0.5より小となって行くような実数を求めよということである。a_nの求め方も難解であるが、記数法の理論とはあまり関係ないので入試問題の解答集にゆずることにして、αを求めてみよう。まず2進法の小数について考え方を整理しておこう。

(1)2倍すると小数点が右にずれる。

(2)次のことは同値である。
　　10進法表示で小数部が0.5より大（小）⇔2進法表示すると小数第1位が1(0)

αは2倍、2倍して行くと、小数部分が0.5より小、大と交互に変化するので、2進法表示すると小数点以下が交互に0,1となっていることになる。そこで
　　　α＝0.0101010101・・・₍₂₎
とおける。
よって、
α＝(1/2)²＋(1/2)⁴＋(1/2)⁶＋・・・＋
　＝(1/4)/(1-1/4)＝1/3