記数法の変換
記数法の変換
(1)K進法表示からm進法表示へ
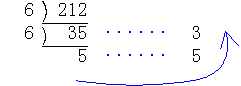
324(8)を6進法表示することを考える。
212=552(6)
この例のように一度10進法表示という媒介を経て、8進法表示から6進法表示に変換するのも良いが直接8進法から6進法に変換するのはどうのようにすればよいのだろうか。
まず、(ア)の式を考えてみよう。
或いは次のような方法も可能である。
(イ)の方法で、6で割って商と余りを求め、その商を再び6で割って商と余りを求める操作を続けていくと順次an、an-1、・・・、a1、a0が求められる。ただし、左辺の324(8)を6で割ってゆくことになるので8進法の計算で、6で割るというわり算を順に行えばよいのである。
逆に552(6)を8進法表示するのも同様に2通りの考え方のいずれでも可能である。
としても良い。
(解)0.21213(6)=a1×1/8+a2×1/82+a3×1/83+・・・とおくと両辺に8を掛けて整数部分がa1であり、小数部分はa2×1/82+a3×1/83+・・・と等しいとおける。このようにして順次a1、a2、a3、・・・を求めてゆく。この場合両辺に次々と掛けてゆくのは8であるが、右辺は6進法表示のままなので8=12(6)を掛けるのである。
(解)0.26(8)=a1×1/6+a2×1/62+a3×1/63+・・・とおいて前の例と同様にb1、b2、b3、・・・を求めていけばよい。しかし、ここではもう一つの別な方法で求めてみよう。
0.26(8)=2×1/8+6×1/82=(2×8+6)/(1×82)
(2)K進法表示からKn進法表示へ
2進法表示から4進法表示とか8進法表示への変換、或いは3進法表示から9進法表示への変換というように、一般にK進法表示からKn進法表示への変換は更に簡単な方法がある。もちろん(1)で考察した方法で可能であることはいうまでもないことであろう。まず(1)の方法で11011101(2)を8進法表示してみよう。
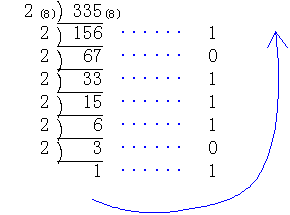
11011101(2)=a0×8n+a1×8n-1+a2×8n-2+・・・+an-1×8+anとおいて次々と8で割ってゆくとan、an-1、・・・、a1、a0が求められる。ただし、8で割るのは2進法での算法で行うので除数8を100(2)として計算することに注意すればよい。このようにしてa0=11(2)=3、a1=11(2)=3、a2=101(2)=5であるから11011101(2)=335(8)となる。逆に335(8)を2進法表示する場合も同様に335(8)=a0×2n+a1×2n-1+a2×2n-2+・・・+an-1×2+anとおいてan、an-1、・・・、a1、a0を求める。この場合は8進法の除法で求めることになる。
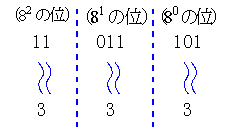
ところでK進法表示からKn進法表示への変換は、もっと簡単で機械的に計算し得る方法がある。11011101(2)を8進法表示するときには8=23より2進数を下から3桁ごとに区切って次のようにすればよい。
11:011:101(2)と区切り、このときの11,011,101は2進法表示でそれぞれ3,3,5を表しているのでこれをもとにして335(8)とすればよい。
また4進法表示するには4=22より2桁ごとに区切ってゆけばよい。
このようにして11011101(2)=3131(4)となる。これは次の計算より明らかであろう。
11011101(2)=1×27+1×26+0×25+1×24+1×23+1×22+0×21+1
一般にK進法表示からKn進法表示に変換する場合には、K進法表示された数を下からn桁ごとに区切って行けばよい。
逆に335(8)を2進法へ、31314を2進法へ変換させることを考えよう。前の式変形を逆にたどってみよう。
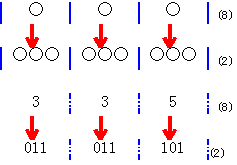
8進数の3桁目、つまり82の位までの最小数は1×82=100(8)であり、これを2進数に変換させると1×82=1000000(2)となり2進法では7桁の数である。また8進数の82の位での最大の数は7×82であり、これを2進数で表すと7×82=111000000(2)となり9桁の数である。よって、8進数の3桁目の数は2進法では7桁目から9桁目までの間の数で表すことができる。同様に考えてゆくとき8進法での81の位の数は2進法では4桁から6桁までの間で表すことができ、8進法での1の位の数は2進法で1桁から3桁までの数で表される。では335(8)を2進法に変換する簡便計算を考えよう。8進法で使われる各位の数字は0,1,2,・・・,7の8個であり、これを2進法で表すとき3桁の2進数として表すことにする。0は000(2)、1は001(2)、2は010(2)、・・・、7は111(2)である。この場合0や1でも000(2)、001(2)のように必ず3桁で表すのである。こうして8進法の各位の数字を3桁の2進数に直しつつ順に並べて書いてゆくと良い。
335(8)の場合82の位の3、81の位の3、1の位の5を順に2進法に直し、011:011:101(2)とすれば良いのである。最高位の0だけは最後に省いて11011101(2)となる。
図示すると次のような関係がある。
同様にして4進数を2進数に直すのであればそれぞれの数字を2桁の2進数で表すようにすればよい。
普通の数を2進法表示する場合、桁数が非常に多くなり煩雑であるが、一度に8進法表示してから上記の方法で2進法に直すと簡単である。
(ア)324(8)=3×82+2×8+4=212
この212を6進法で表す。
(イ)
324(8)=3×82+2×8+4
この式の右辺の3=3(6)、2=2(6)、4=4(6)に注意すると
324(8)=3(6)×122(6)+2(6)×12(6)+4(6)
=3(6)×144(6)+24(6)+34(6)
=520(6)+24(6)+4(6)=552(6)
となる。つまり、6進法の乗法と加法を利用することになる。
324(8)=a0×6n+a1×6n-1+・・・+an-1×6+an
とおいて、このa0、a1、a2、・・・、anの値がわかれば324(8)の6進法表示が明らかにされる。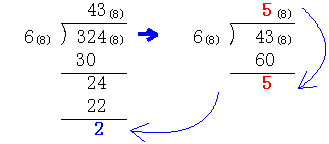
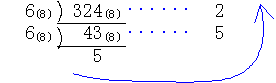 ∴324(8)=552(6) となる。
∴324(8)=552(6) となる。
552(6)=5×62+5×6+2
=5(8)×62+5(8)×6(8)+2(8)
=5(8)×44(8)+36(8)+2(8)
=264(8)+36(8)+2(8)
=324(8)
次に8=12(8)に注意して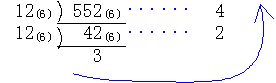 ∴552(6)=324(8)
∴552(6)=324(8)
(例10)0.20213(6)を8進法表示せよ。
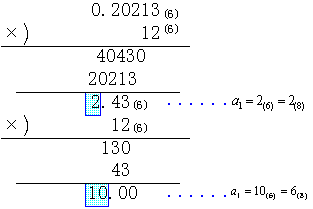
(例11)0.26(8)を6進法表示せよ。
=26(8)/100(8)=34(6)/144(6)
=0.20213(6)

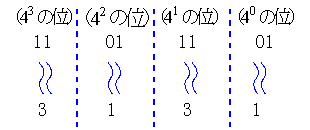
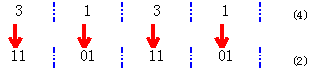
11011101(2)=1×27+1×26+0×25+1×24+1×23+1×22+0×21+1
=(1×2+1)26+(0×22+1×22+0+21)+1
=3×82+3×81+5
=335(8)
=(1×2+1)26+(0×2+1)×24(1×2+1)×22+0×21+1
=3×43+1×42+3×4+1
=3131(4)
335(8)=3×82+3×8+5
=(1×2+1)26+(0×22+1×2+1)23+1×22+0×21+1
=1×27+1×26+0×25+1×24+1×23+1×23+1×22+0×21+1