 1次変換の重要性質
1次変換の重要性質
(1)1次変換で変わらないもの
(2)1次変換で変わるもの
(3)(0,0),(1,0),(0,1)をO(0,0),A,Bに移す1次変換が存在する。この場合O,A,Bの3点は同一直線上にないものとする。
1次変換によって一般に図形は形の異なる図形に移る。(恒等変換もあるが、ここでは考えない。)つまり図形を書き直すときに、そのもとになる1次変換に従って図形を書き直すと考えることにしよう。したがって図形を書き直すときには前述の(1),(2),(3)の1次変換の性質を踏まえた図の書き直し方をすれば、もとの図形を書き直した図形に移す1次変換を想定することができる。
そこである図形を考え、このもとになる図形に対して(1),(2),(3)の性質をふまえて図を書き直した結果、正六角形の図形が得られたとしよう。つまりもとになる図形を正六角形に移すような1次変換を想定しよう。このもとになる図形として次の図のような六角形を考えよう。(もちろんこの六角形は正六角形ではない。)
①同一直線上の二つの線分の比
②平行な二つの線分の比
③二つの図形の面積比
④2直線が平行である性質
⑤2直線が交わる性質
⑥ベクトルの1次式
⑦重心
①線分の長さ
②図形の面積
③2直線のなす角度
④点の座標
⑤直線、曲線の方程式
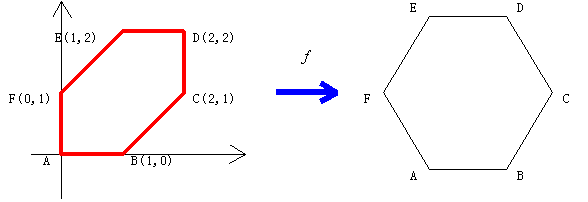
左の図が1次変換fによって右の正六角形ABCDEFに移されていると考えよう。角線分どうしの平行な関係は左の図と右の図とでは全て保たれている。左側の図は各点が簡単な数値の座標で示され、したがってまた各点の位置ベクトルでも簡単な成分で表される。よって左側の図をもとにしてベクトルどうしのいろいろな計算を行い(これは簡単な計算ですむ場合が多い。)、その結果が1次変換によって正六角形ABCDEFの図の上にどのように移されていくかを考えると良い。このことによって正六角形の図の上で成り立つようなベクトルの性質が、間接的ではあるが左側の図をもとにした簡単な計算によって明らかにされるということが可能となる。
ここで例をあげて考えてみよう。