 <例1>
<例1>
|
□の中に適当な数値を入れよ。
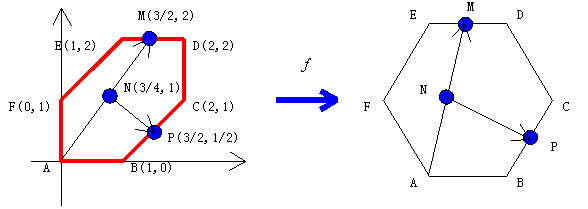
正六角形ABCDEFにおいて、DEの中点をM、AMの中点をN、BCの中点をPとする。このとき |
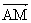 、
、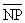 を
を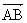 と
と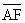 で表す式は1次変換の性質(1)の⑥により、右図の正六角形の図の上でも成立する。よって左図をもとにして
で表す式は1次変換の性質(1)の⑥により、右図の正六角形の図の上でも成立する。よって左図をもとにして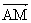 を
を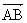 、
、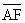 で、同じく
で、同じく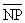 を
を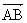 と
と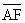 で表してみよう。
で表してみよう。
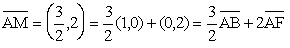
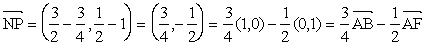
この式は右の正六角形においても成り立つから題意による左図をもとにした計算によって求められたことになる。そしてまた、この解法は実際の正六角形の図の上で考察するよりも易しいのである。
以上述べたことは一つの例であるが、要するにベクトルに関する問題を、図を書き直していわばデフォルメされた図をもとにして、もともとの問題を解いていくように工夫してみようということなのである。この場合、図を書き直すということは1次変換にもとづいて図を書き直すということなのであるから、勝手気ままに図を書き直すことはできない。1次変換の重要性質をふまえた図の書き直しが必要なのである。
そこで図を書き直す場合の注意事項をまとめてみよう。