 <例6>
<例6>
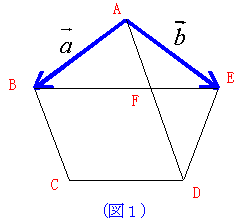 1辺の長さが1の正五角形ABCDEがあり、ADとBEの交点をF、
1辺の長さが1の正五角形ABCDEがあり、ADとBEの交点をF、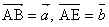 、ADの長さをlとする。 、ADの長さをlとする。(1) 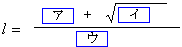 であるから であるから と表せる。 と表せる。(2)  である。 である。 |
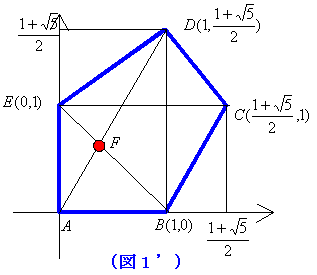
ADとBCは平行なので、ADとBCの線分比が判ればlを求めることができる。線分と線分の平行な関係や、ベクトルの1次式は図を書き直しても変わらないから(図1’)を用いる。
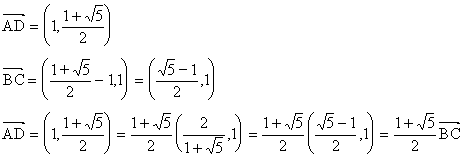
1次変換fによって(図1’)から(図1)に移るとすると、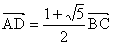 で
で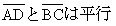 となる性質は(図1)においても成り立つから
となる性質は(図1)においても成り立つから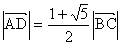 となる。
となる。
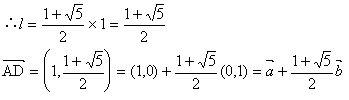
直線ADは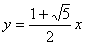 、直線BEはx+y=1、この2直線の交点Fは
、直線BEはx+y=1、この2直線の交点Fは
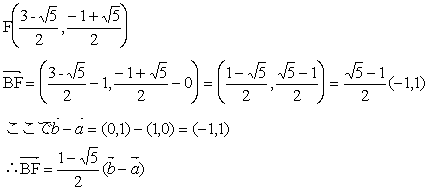
以上の例で見てきたように(図1)から(図3’)までの図を頭の中に入れておくと、問題に応じて1次変換の性質を思い起こしつつ、ベクトルの問題を解いてゆくことができる。
特に正多角形の幾何学的性質をあまり意識しなくとも、単純な成分計算で解いてゆけるので、問題解決の方針も立てやすいのである。