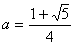<例5>
<例5>
座標平面上の原点Oを中心とする半径1の円に内接する正五角形の頂点を順にP0,P1,P2,P3,P4とする。ただし、P0の座標は(1,0)である。この正五角形を用いてcosπ/5の値を求めよう。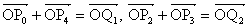 とするとき、点Q1,Q2は直線OP0上にある。 とするとき、点Q1,Q2は直線OP0上にある。したがって、 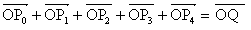 によって定まる点Qは直線OP0上にある。同様にして、点Qは直線OP1上にあることもわかる。したがって点Qの座標は  である。 である。ゆえに、a=cosπ/5,b=cos2π/5とおくと 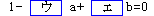 が成り立つ。 が成り立つ。さらに、余弦定理より  であり、 であり、また、 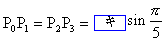 であるから であるから
 が成り立つ。 が成り立つ。よって、 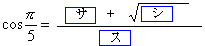 である。 である。
|
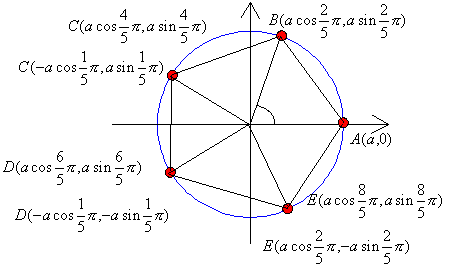
点の座標が指定されているので(図1)を用いて考えることにすればよい。
下の図のABCDEがそれぞれP0,P1,P2,P3,P4でa=1の場合として考えると良い。
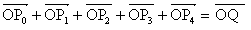 とすると、
とすると、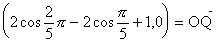
点QはOP0上にあり、かつOP1上にもあるとすると、QはOP0とOP1との交点、つまりOでなければならない。
よって、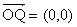 。ゆえにQ(0,0)
。ゆえにQ(0,0)
よって、2cos2π/5-2cosπ/5+1=0・・・①
cos2π/5=b,cosπ/5=aとおくと、2b-2a+1=0・・・②
△OP0P1について余弦定理を適用する。
P0P12=12+12-2×1×1cos2π/5
∴P0P12=2-2b・・・③
更に正五角形であるから
P0P1=P2P3
=sinπ/5-(-sinπ/5)=2sinπ/5
∴P0P12=4sin2π/5
=4(1-cos2π/5)=4(1-a2)・・・④
④を③に代入して、2-2b=4(1-a2)
これに②より2b=2a-1を代入。2-(2a-1)=4(1-a2)
∴4a2-2a-1=0、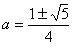
cosπ/5>0より