 練習問題 x秒後の瞬間速度ym/秒が y′=xで表わされる斜面の落下運動について、2秒後から5秒後までの間にころがる距離を求めなさい。
練習問題 x秒後の瞬間速度ym/秒が y′=xで表わされる斜面の落下運動について、2秒後から5秒後までの間にころがる距離を求めなさい。
速度から距離を求める
これまでは距離の式から瞬間速度を求めてきたが、ここで逆に速度の式から距離を求めることを考える。
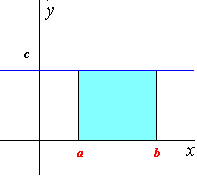
等速運動の場合、その進む距離は速度×時間で右の図のような長方形の面積で表わされる。
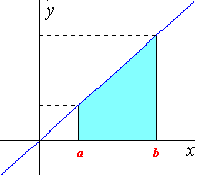
この問題のような速度の変化する運動の場合、その進む距離は、瞬間速度y′と無限小時間dxとの積 y′×dx を無限に加えたものであるから、 これを 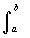 y′dx と表わす。
y′dx と表わす。
これは第Ⅰ部でやったグラフの下の面積であり、一般的には積分で求められる。
こうして、速度の式から距離を求める積分と、距離の式から速度を求める微分は、ちょうど逆の関係になっている。
微分してf(x)になる関数F(x)をf(x)の原始関数という。
この記号をつかえば第Ⅰ部の定積分は次のように表わすことができる。
微積分学の基本定理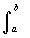 f(x)dx=F(b)-F(a) f(x)dx=F(b)-F(a)
|