ｎが有限のときには10000等分の100000等分・・・のようにいくらｎを大きくしても、ｆ（ｘ）のしたの面積の値と、リーマン和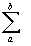ｆ（ｘ）Δｘとの差はほんのわずか残る。

　そこで逆にｆ（ｘ）の下の面積の値というのは、ｎを無限にしてΔｘを無限小にした場合のリーマン和であると考える。

　つまりｆ（ｘ）の下の面積というものを、分割の幅Δｘを無限小ｄｘにしたｆ（ｘ）・ｄｘを無限に加えた和で定義する。
　　　Ｓ＝ｆ（ｘ）・ｄｘ＋ｆ（ｘ）・ｄｘ＋・・・無限・・・＋ｆ（ｘ）・ｄｘ

　これをｆ（ｘ）のａからｂまでの定積分といい
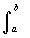　　　　　　ｆ（ｘ）ｄｘ　　と表わす。
　　　　（インテグラルａからｂまでのｆ（ｘ）ｄｘとよむ）

例　ｆ（ｘ）＝ｘ^２の０から１までをｎ等分するとき　そのリーマン和は
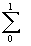　　　　ｘ^２・Δｘ＝

　ここでΔｘ＝１／ｎをどんな実数よりも小さい無限小にしそれをｄｘと表わせば
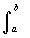　　　ｘ^２・Δｘ＝

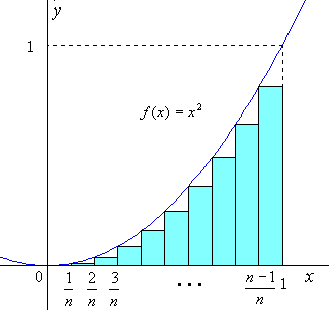
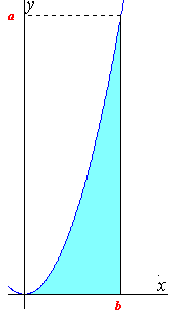問題　次のグラフはｆ（ｘ）＝ｘ^２のグラフである。このｆ（ｘ）の０から、ある点ｂまでの定積分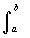ｘ^２ｄｘの値を予想しなさい。
　　　　　　（ヒント　　たてｂ^２　よこｂの長方形の面積はｂ^３）