俀丏儕乕儅儞榓
丂傢傟傢傟偼丂偙偺倖乮倶乯偺壓偺椞堟傪摍偟偄暆偵愗偭偰丄崅偝倖乮倶乯偺嵶挿偄挿曽宍傪偮偔傝丄偦偺柺愊偺榓傪峫偊傞丅
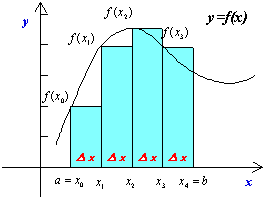
丂椺偊偽嬫娫乵倎丄倐乶傪係摍暘偟偰丄偦傟偧傟偺忋偵崅偝倖乮倶侽乯倖乮倶侾乯倖乮倶俀乯倖乮倶俁乯偺挿曽宍傪偮偔傞丅
丂偙傟傜偺挿曽宍偺柺愊偺榓偼丂彫嬫娫偺暆乮倐亅倎乯乛係 傪儮倶偲昞傢偣偽丄
丂丂丂倖乮倶侽乯丒儮倶亄倖乮倶侾乯丒儮倶亄倖乮倶俀乯丒儮倶亄倖乮倶俁乯丒儮倶 偲側傞丅
栤戣丂倎亖侾丂倐亖俆偱 係摍暘乮儮倶亖侾乯偟偨偲偒偺偙偺挿曽宍偺柺愊偺榓傪媮傔傛丅
丂偙偺傛偆側挿曽宍偺榓傪倖乮倶乯偺倎偐傜倐傑偱偺儕乕儅儞榓偲偄偄丄
丂丂丂丂丂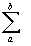 倖乮倶乯丒儮倶 偱昞傢偡
倖乮倶乯丒儮倶 偱昞傢偡
掕媊丂倖乮倶乯偺倎偐傜倐傑偱偺儕乕儅儞榓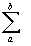 倖乮倶乯丒儮倶亖倖乮倶侽乯丒儮倶亄倖乮倶侾乯丒儮倶亄倖乮倶俀乯丒儮倶亄丒丒丒丂亄倖乮倶値亅侾乯丒儮倶 倖乮倶乯丒儮倶亖倖乮倶侽乯丒儮倶亄倖乮倶侾乯丒儮倶亄倖乮倶俀乯丒儮倶亄丒丒丒丂亄倖乮倶値亅侾乯丒儮倶丂丂乮偨偩偟倶侽亖倎丂倶値亖倐丂儮倶亖 乮倐亅倎乯乛値丂乯 |
丂偙偺儕乕儅儞榓偼壓偺恾偺傛偆偵値傪偳傫偳傫戝偒偔乮儮倶傪偳傫偳傫彫偝偔乯偟偰偄偗偽丄倖乮倶乯偺倎偐傜倐傑偱偺壓偺柺愊偵偳傫偳傫嬤偯偔偱偁傠偆丅
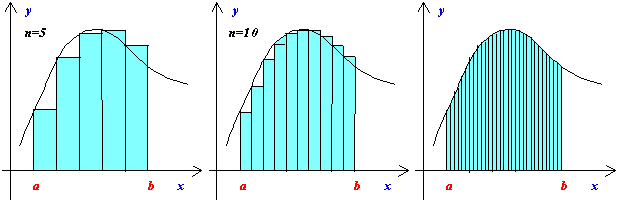
丂偙偺偙偲傪丂倖乮倶乯亖倶俀丂偺侽偐傜侾傑偱偺壓偺柺愊偵偮偄偰妋偐傔偰傒傛偆丅
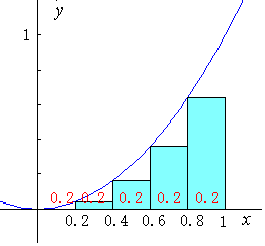
値亖俆偺偲偒
丂丂丂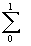 倶俀丒0.2亖侽俀丒0.2亄0.俀俀丒0.2亄0.4俀丒0.2亄0.6俀丒0.2亄0.8俀丒0.2亖
倶俀丒0.2亖侽俀丒0.2亄0.俀俀丒0.2亄0.4俀丒0.2亄0.6俀丒0.2亄0.8俀丒0.2亖
丂値亖侾侽偺偲偒
丂丂丂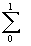 倶俀丒0.1亖0俀丒0.1亄0.1俀丒0.1亄0.2俀丒0.1亄
倶俀丒0.1亖0俀丒0.1亄0.1俀丒0.1亄0.2俀丒0.1亄
摨條偵寁嶼偡傞偲
丂値亖俆侽偺偲偒丂丂丂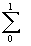 倶俀丒0.02亖丂侽丏俁俀俁係
倶俀丒0.02亖丂侽丏俁俀俁係
丂値亖侾侽侽偺偲偒丂丂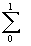 倶俀丒0.0侾亖侽丏俁俀俉俁俆
倶俀丒0.0侾亖侽丏俁俀俉俁俆
丂値亖侾侽侽侽偺偲偒丂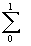 倶俀丒0.001亖侽丏俁俁俀俉俁俁俆丂丂丂丂偲側傞丅
倶俀丒0.001亖侽丏俁俁俀俉俁俁俆丂丂丂丂偲側傞丅
丂偙偺傛偆偵儮倶偵懳偡傞倖乮倶乯偺倎偐傜倐傑偱偺儕乕儅儞榓
丂丂丂丂丂丂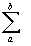 倖乮倶乯儮倶丂丂偼
倖乮倶乯儮倶丂丂偼
暘妱偺悢値傪戝偒偔偡傞偙偲偵傛偭偰儮倶傪偳傫偳傫彫偝偔偟偰偄偗偽丄倖乮倶乯偺壓偺柺愊偵嬤偯偄偰偄偔偱偁傠偆丅
幙栤丂暘妱偺悢値傪戝偒偔偟丄儮倶傪偳傫偳傫彫偝偔偟偰偄偗偽丄儕乕儅儞榓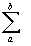 倖乮倶乯儮倶丂丂偼倖乮倶乯偺壓偺柺愊偺抣偲偄偮偐偼堦抳偡傞偩傠偆偐丅
倖乮倶乯儮倶丂丂偼倖乮倶乯偺壓偺柺愊偺抣偲偄偮偐偼堦抳偡傞偩傠偆偐丅
丂梊憐丂傾丏偄偮偐偼堦抳偡傞丂丂僀丏偄偮傑偱傕堦抳偟側偄丂丂僂丏偳偪傜偲傕偄偊側偄