侾丏嬋慄恾宍偺柺愊應搙
丂戞侾晹偱傢傟傢傟偼捈慄恾宍偺柺愊傪掕媊偟丄偦傟偵應搙傪梌偊傞偙偲偑偱偒偨丅偙偺戞俀晹偱偼嬋慄恾宍偵偮偄偰偦傟偵柺愊應搙傪梌偊傞偙偲傪峫偊傞丅
丂娙扨偵偡傞偨傔師偺恾偺傛偆偵丄嬋慄偵埻傑傟偨恾宍傪偄偔偮偐偵暘妱偟丄堦曽偩偗偑嬋慄偵埻傑傟偨恾宍偵懳偟偰丄柺愊應搙傪梌偊傞偙偲傪峫偊傞丅
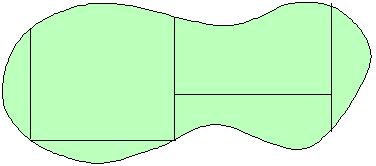
丂傢傟傢傟偼丄恾偺傛偆側嬋慄傪娷傓恾宍偵懳偟偰丄掙曈傪倶幉偵偟丄揰倶偵懳偡傞崅偝傪倖乮倶乯偲昞偡丅恾偺傛偆偵丄嬋慄倷亖倖乮倶乯偲俁偮偺捈慄丄倶亖倎丂倶亖倐丂倶幉偵傛偭偰埻傑傟偨椞堟偵柺愊應搙傪梌偊傞偙偲傪峫偊傞傢偗偱偁傞丅
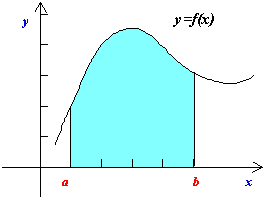
偙偺偲偒丂倷亖倖乮倶乯偺偟偨偺倶亖倎偐傜倶亖倐傑偱偺柺愊應搙傪
丂丂丂丂丂丂俵乮倎丆倐乯丂丂丂偲偁傜傢偡偙偲偲偡傞丅
幙栤丂偳偺傛偆側曽恓偱峴偗偽丄倖乮倶乯偺壓偺椞堟偵柺愊應搙傪梌偊傞偙偲偑偱偒傞偲峫偊傑偡偐丅