2.面積測度
次にわれわれはこの直線図形の面積の大きさを数で表わすことを考える。このとき前節の結論から長方形の面積が数で表わされれば十分である。ある量の大きさを数で表わすことを、その量に測度を与えるという。われわれはこれから長方形の面積に測度を与えることを考えるわけである。
長方形はたての長さL1と横の長さL2によって決まる。そこでこの長方形の面積を M(L1、L2) と表わすこととする。このとき当然
| Ⅰ M(L1、L2)=M(L2、L1) |
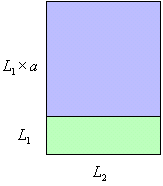 またすべての長方形はよこの長さを等しくして、たての長さで面積を比較できた。このときたての長さと面積は比例している。すなわちたての長さを2倍3倍・・・とすれば、面積も2倍3倍となる。
またすべての長方形はよこの長さを等しくして、たての長さで面積を比較できた。このときたての長さと面積は比例している。すなわちたての長さを2倍3倍・・・とすれば、面積も2倍3倍となる。
| Ⅱ M(L1×a、L2)=M(L1、L2)×a |
さらにⅠとⅡから
| Ⅱ´M(L1×a、L2×b)=M(L1、L2)×a×b |
これを面積の複比例構造とよぶ。
質問 長方形の面積に測度を与えるには、どうすればよいか。
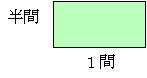
例えば家の部屋の面積を表わす単位としては、たて半間よこ1間の長方形
M(半間、1間)=畳 がよく用いられる。
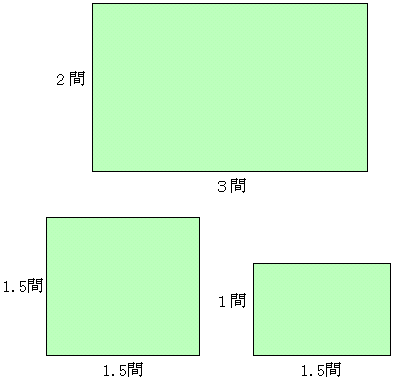
問題 次の長方形の面積を畳を単位として求めなさい。
質問 もとの単位となる長方形はどのようなものでもよいのだが、どんな長方形を単位にすると計算に便利だと思いますか。
問題 次の長方形の面積を M(1間、1間)=坪 を単位として求めよ。
① M(6間、7間)=
② M(3間、6間)=
③ M(10間、10間)=