※以下、文中で●とあるのは、画像ファイルが不鮮明で活字が読みとれなかった部分です。
単元８ 文明の進歩に数学はどんな役割をしたか
現在私たちは高度に発達した文明のなかに生活しているから、数学が私たちの生活にどんなにたいせつであるかといわれても、電気がどんなにたいせつであるかといわれたほどには実感が出ない。一般に、私たちが絶えず使っているもののありがたさを忘れやすいのは、空気や水や日光のありがたさに気がつかないようなものである。私たちが絶えず使っている加減乗除の計算や、算用数字による数の記法、簡単な幾何学的知識もこれと同じで、その重要さに気がつかないのである。
このようなことの重要さを知るためには、それが発明されなかったころのことを、または発明された当時のことを考えてみればよい。たとえば日本では室町時代の末、ヨーロッパでもほぼそのころに当たるルネッサンスの初期において、計算はむずかしい技術であった。豊臣秀吉のころの人である毛利勘●衛は、その数学書の中で割算の仕方を説明し、巻末に「われこそは割算の日本一と称するものなり」と書いている。割り算のうまいことをじまんできるほどに割算はむずかしい技術だったのである。
この単元では文明の発達の歴史から、つぎのようなことをとり出して、数学が文明の進歩にどんな役割をしたかしらべてみよう。
１．古代東方諸國と数学
太古の人類は小さな集團をなして生活し、野獣と戦い、毎日の生活に追われながらくらしていたものであろう。やがて集團が大きくなり、安住して農耕や牧畜をおこなうようになり、生活にゆとりができ、規則正しい生活がはじまるようになって文化が起こってくる。かくして経験や知識はしだいに蓄積され、新しい道具や技術は発明され、それらはますます人の生活を安定させるとともに、社会全体が日常生活のみに追われることがなくなる。
また原始人の死に対する恐怖、外界の現象に対する驚異、現在および将来の幸福や霊魂の不滅を願う心などは宗教をつくり出し、僧りょの階級は人の精神を支配するようになった。しかも、その支配力は精神界のみならず政治、経済にもおよび、ここに宗教的な國家が生ずる。
このようにしてできた強力な國家は人の物心両面を支配して、大土木事業を起し、またそれに必要な税金をとりたて、ここに整備された國家組織ができる。このような土木事業や行政的組織は、それに必要な多くの技術や知識を産みだす原因となり、また一方日々の生活に追われぬ僧りょ階級のものは、これらの知識を蓄積し整理するのに役立ったであろう。このようにして、現実的な要求と精神的な要求とをもとにして、学問はできてきたのである。
課題１．文明はどのように発生したかをしらべてみよう。
世界で最も古く文明が起ったのは、チグリス・ユーフラテス川の流域であるメソポタミア地方であり、つぎにナイル川の流域であるエジプト地方であるといわれる。これらの地方はいずれも、太古の人類が生活にゆとりを見出だすのに適していたものであろう。
メソポタミア地方の文明については、歴史に伝わることが少なく、１９世紀以後の発展ときっ形文字の解釈とによって、はじめて人々に知られるようになってきた。この地方は石に乏しかったため、土木事業はれんが（そのなかには、日ぼしれんがも多かった）でおこなわれ、それらは長年の風雨に土の山と化してしまった。
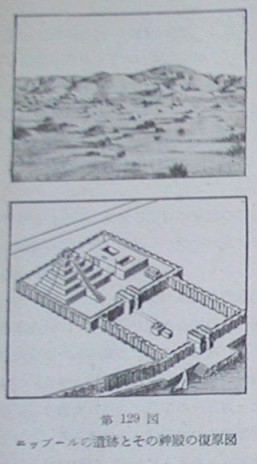しかしその遺跡から想像すると、それらの構築物は壮大なものであったらしい。したがって、それを作った当時の力学的・幾何学的知識の豊かさも想像できるが、今日では精確には知ることができない。私たちはただきっ形文字で書かれた文書を解読することによって、当時の学問の一部を知ることができるのみである。
課題２．スメル・バビロニア・アッシリアの歴史や遺跡についてしらべよう。
バビロニアでは数を６０進法と１０進法との混用によって表わし、また三角形・長方形・台形の面積が計算され、円周率としては３が用いられていた。代数的方面はとくに進歩していたらしく、６０進法による計算法が考案され、一次と二次の方程式が解かれていた。また天文の観測がおこなわれ、星座表が作られ、日食・月食の周期が知られていて、その予言がおこなわれていた。
天文学というものは最も早く発達した科学であって、原始人にとって星や太陽や月の運行の規則正しさは驚異の的であったのであろうし、四季の移り変わりを知るためや、さばくを旅行するときに方角を知るための必要からも、その発達がうながされたのであろう。星の運行が予言できることと、星の運行が四季の移り変わりに関係あることは、人々に星の運行から●の現象の予言もできるであろうと●●させたのであろう。メソポタミアではとくにこれが盛んで、天文学は●●●と●●●をもっていたらしい。
これは古代人に共通のことであって、中国の五行（水・火・●・金・●）や、千三支は天文学と関係の深いものであったろうが、後には全くうらないや●●となり、わが國でも黄道吉日などの●にその跡を残している。また、奈良時代に●の文物を編入したとき、数学や天文学も編入されたのであるが、それらは●●の学といううらないの一種と肩を並べるものであった。
科学の本質を理解せずに、その形式的結果のみを濫用すると、うらないや迷信に化することがあることを私たちは現在も注意しなければならない。
課題３．古代天文学の歴史をしらべてみよう。
課題４．科学的な知識が誤解されて迷信になっている例をあげてみよう。
人が数を１０進法で表すのは、私たちの手の指が５本であるのに基づくのであるが、バビロニア人が６０進法を用いた理由は何によるのであろうか。６０は２、３、４、５、６等の数で割り切れるし、１年は約３６５日、１月は約３０日、１年は約１２月（月の運行で測って）等のことから、６０進法のつごうのよい点は確かにあったのであろう。そしてそのなごりを今日でも時間と角度の単位に残している。
エジプトについてはギリシア人が多くの記録に残しているうえに、その壮大な石造の遺跡が、そのまま後世まで残っていたために古くから人々がその文化の古さを知っていた。しかし、エジプトについて種々のことがわかりはじめたのは、やはり１９世紀後半以後のことで、ロセッタ石の解読に始まるエジプト文字の解明と、いくつもの考古学的発掘とによるのである。
課題５．エジプトの歴史や文明や遺跡についてしらべてみよう。
２．ギリシアの数学
ギリシアの地には古く紀元前３０００年ごろから、クレタ島を中心とするいわゆるエーゲ海文明が開けていた。ギリシア人（かれらは自分たちのことをヘレネスと呼んでいた）は紀元前１０００年ごろを中心として数百年の期間にわたっておもむろに北方からギリシアの地に侵入し、当時すでにおとろえつつあった先住民族をあるいは追い、あるいは服従してここに定住するようになった。
ギリシアの地は山が海岸までせまり、また海は無数の入江となって陸地に入りこみ、大きな平地はなく、陸地の交通は不便であり、天産物にも乏しかった。ギリシア人は入江の奥の小平野や、山中の盆地や、エーゲ海にある多くの島々に、神殿を中心として城壁に囲まれた小さな都市国家を作った。これがポリスである。
ギリシア人は各自のポリスを基地にして、勇敢に地中海に乗り出し、東方諸國と交易し、南部イタリア・シシリー・小アジア・黒海の沿岸に植民地を作っていった。かれらはかくして東方諸國の文明を吸収するとともに、やがて独自の文明を作り上げたのであった。
ギリシアの地は気候が温和で、雨が少なく、空気は乾燥し、青い空と海とを背景にして、強い日光の下ですべてのものは明かるくはっきりと形を現している。
この風土の影響を受けてか、ギリシア人は神秘的な内にこもったようなものでなく、明かるく、はっきりと形をもったものを喜び、合理的に物事を考えた。かれらの彫刻や建築が均整のとれた、明かるい、合理的なものであったのと同じく、かれらは数学のなかでも、はっきりと形をもった図形を対象とする幾何学を重んじ、均整のとれたギリシア幾何学を作り上げたのである。
課題１．ギリシアの歴史・地理・文化につき皆で分担してしらべてみよう。
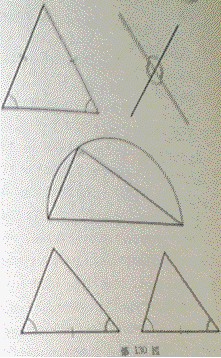ギリシア文明はまず東方諸國●●●●●●●●●●●●●●●●●。ギリシアの学問の始源と呼ばれるタレス（紀元前６００年ごろ）は小アジアのミレトスの生まれである。
タレスは商業の目的でフェニキァやエジプトに旅行して数学や天文学を学んだといわれている。かれの業績は正確に伝わっていないが、幾何学についてはつぎのことを発見したといわれる。すなわち、
１）二等辺三角形の両底角は相等しい。
２）二直線が交わって作る相隣らない角（対頂角）は相等しい。
３）円の直径を１辺とし、円周上に１頂点をもつ三角形は直径を斜辺とする直角三角形である。
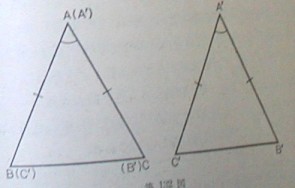
４）二つの三角形の対応する２角がそれぞれ等しく、かつ対応角のはさむ辺の長さが等しければ、両三角形の他の対応角・対応辺も皆等しい。
また、かれは円が直径により２等分されることを証明し、比例の理を用いて海岸の１点から海上の舟までの距離を測り、ピラミッドの高さをその影によって測定したと伝えられる。かれは万物を水であると説いたといわれる。自然にあるものを神話によらずに合理的に説明しようとした試みとして、時代を画するものといわなければならない。
ピタゴラス（紀元前６世紀）も小アジア沿岸のサモス島の生まれで、エジプトやバビロニアに旅行して学び、のちに南イタリアのクロトンに宗教的な●●を●●したといわれる。かれに関することは早くから伝説化され、かれとその学派との業績を
３．ユークリッド幾何学
先にタレスのところであげた、直径を１辺として円周上の１点を頂点とする三角形は直角三角形であるということについて考えてみよう。これは二等辺三角形の両底角が等しいこと、三角形の内角の和が２直角に等しいことの二つから導くことができる。
いまＯを中心とする円の一つの直径をＡＢとし、円周上の１点をＣとする。∠ＡＣＢが直角であることを示せばよい。さて、ＯとＣとを結べば、円というのは中心にコンパスの１端をおき、コンパスの開きを変えずに他端でかいた図形だから、中心から円周上に至る距離はすべて等しい。したがって、ＯＡ＝ＯＣ＝ＯＢである。そこで △ＯＡＣ、△ＯＣＢはともに二等辺三角形になり、両底角はそれぞれ等しい。それをα、βと置けば
∠ＯＡＣ＝∠ＯＣＡ＝α、∠ＯＣＢ＝∠ＯＢＣ＝β。
ゆえに∠ＡＣＢ＝α＋βとなる。△ＡＢＣの内角の和は
∠ＢＡＣ＋∠ＡＣＢ＋∠ＣＢＡ＝α＋（α＋β）＋β＝２（α＋β）
となり、三角形の内角の和は２直角であるから、２（α＋β）が２直角となり 、（α＋β）は直角となる。これで証明がすんだのである。
さて、この証明をふりかえってみると、円周上の点は中心から等距離にあること、二等辺三角形の両底角は相等しいこと、三角形の内角の和は２直角に等しいことを使っている。このうち、円周上の点が中心から等距離にあるというのは、中心から等距離にある点の全体を円周というのであることから当然であって、二等辺三角形の２辺は相等しいというのと同様である。
性質ＢをもつものをＡと名づければ、ＡがＢという性質をもつのは当然なことである。ものに名前をつけただけで新しい事象が発見されるわけはないが、適当に名前をつけることによって私たちがものをのべる手間が非常に省けるばかりではく、ある性質の組み合わせに一つの名前をつけておけば、その名前をつけられたものがいろいろな重要な役目をすることが多い。たとえば、株式会社という名前を使わなかったならば、私たちはどんなに困るであろうか。
私たちが植物を分類し、顕花植物・被子植物・双子植物などという。これらはいずれもある性質をもつものにつけられた名前である。このようにある性質をもつものに名前をつけることを定義するという。名前がついているからその性質をもつのではなく、元来はその性質に対して名前がつけられたのであることを忘れないでほしい。
問１．定義の例をあげよ。
課題１．定義したために、非常に利益を得た経験があったらば発表しよう。
７．社会と統計
私たちは１７世紀に急速に発展した近世数学が自然科学の発展にかくことのできないものであったというより、近世の数学は自然科学とともに発達したものであったということを知り、その一例として振動と三角函数の関係をしらべたのであるが、１９世紀以後になって数学は自然科学以外のものにも大いに用いられるようになった。
その最もたいせつな例は統計である。統計はもちろん１９世紀になってはじめられたものではない。しかし、統計が積極的に大きな意味をもち出したのは１９世紀以来である。
文藝復興期以後、航海術の進歩、新大陸の発見、機械の発明等により、ヨーロッパの人口は増し、産業は盛んになっていったがこれに大きな変革を与えたのが、１８世紀後半にイギリスで起った産業革命であった。
１８世紀後半から１９世紀の初めにかけては、政治的には、アメリカの独立、フランスの革命、ナポレオンの戦争等があって多事であったが、工業技術の上でも多くの発明がなされて多事であった。このような影響により、産業の規模は大きくなり、労働者の数は増し、各國はその國力を増すことに力を費した。このような大規模な経済組織によって仕事をするばあいには、どうしても周到な計画が必要になる。それには現在の状態を知ることが何よりたいせつで、かくして統計が必要になってくるのである。
課題１．産業革命についてしらべてみよう。
●世紀末以来の産業技術の進歩は産業革命の比でない。とくに重工業技術の進歩は著しく、電力の利用があらたに加わった。資本は蓄積され、産業の規模はいよいよ大きくなった。統計の重要性は日に日に増している。私たちはすでにこの本のいろいろな●所で統計についてしらべているから、ここでとくに統計についていわないでもよかろう。
８．この単元でしらべたこと、さらに研究したいこと
この単元でしらべたことについて、ここにまとめてみよう。
この単元でしらべた数学的なことがらについてはつぎのようなことがある。
まずユークリッド幾何学の議論の仕方についてつぎのようなことがある。
簡単な幾何学のことがらとしてはつぎのようなものがある。
三角函数のことについてはつぎのことがある。
この単元の参考書として、さきに単元３であげておいた「百万人の数学」の外に、つぎのものをあげよう。
私たちはここで文明の進歩に数学がどんな役割をしたかについて歴史的にしらべたのであるが、インドを除いては東洋のことにふれなかった。その一つの理由は、東洋の数学は現代の文明に対して大きな役割をしていないからである。日本の数学（和算）は特殊な発達をしたものであった。（「百万人の数学」にπの計算についての和算の結果が出ている。これは和算の達したもっともたいせつな結果の一つである。）なぜそのように発達したものが、さらに発達することなく消滅したか。それがどうして日本の文明に大きな役割をしなかったかというと、和算には大きな欠点があったからであろう。そのようなことをしらべてみるのもおもしろいであろう。東洋の数学のことはまだ明らかでない点が多く、適当な参考書がないことは残念である。
【考察】
一つの単元の内容を比較的まとめてデジカメ写真を撮っていた部分を、まず取り上げた。単元の内容としては『数学史』に関わるものである。ただ、バビロニアの６０進法等、『数の表記法』についての記述は、これから使うであろう『数学基礎』の教科書でもふれられているが、明らかに導入の仕方が異なる。公然化前の白表紙本からの記述は差し控えるべき時期でまだあるため、具体的に比較することはできないが、『数学基礎』の教科書ではなぜその学習内容に入るのか、取り組みの必要性を論じている部分が少ない。これが『生活単元学習』の頃の教科書と現代の教科書一般との最も大きな相違点であろう。
およそ、『数学の近代化（あるいは現代化）』と称されて今風の教科書に編修の仕方が変わってからは、数学の教科書には『なぜ、その内容に取り組むのか』『なぜ、数学を学ぶのか』といった部分の論述がなくなってしまった。だから私が過去に勤務してきた学校などでは、数学嫌いの生徒から『なぜ、数学を学ぶのですか』『数学やっても意味ないでしょ』『数学って何に役立つのですか、私進学しないんですが……』って声をたくさん聞いてきた。以前の私はその都度先にあげた教科書の例を出して『生活するために数学って必要なんだ』と答えてきた。でも、なかなか生徒たちは納得しなかったけど……。本校は受験校であるため、生徒はそれなりに勉強し、数学＝受験科目としてとらえている（私個人はそういう生徒に不満をもっているのであるが）。
今回、『数学基礎』という科目が登場し、内容としては過去の『数学一般』のリバイバルに近いものの、教科書だけでは過去のものに比べ、（今の教科書よりはよいものの）面白みに欠ける部分があることは否定できない。そのため、私の前作のレポートのようにインターネットを使ったりして内容をふくらませていくことを提案した。本章で原稿を起こした過去の教科書をみると、『課題』と称する取り組みの内容は数学に関わった内容もあるが、歴史や文化といった数学では扱っていないものも調べることになっており、今で言うところの『総合的学習』にイメージとしては近い。また、『２．ギリシアの数学』の項の課題１．では『皆で分担してしらべてみよう』となっており、現代の画一的（あるいは一斉的）な教育とは異なり、協働型の学習形態に近かったことを示唆していると思われる。
せっかくこのように生活に根ざしたゆとりのある教育を日本は昭和２０年代後半にやっていたのに、『学力が向上しない』という理由から否定され、『詰め込み主義』の教育に変わってしまった。それが、今回、また『反省』という名で否定され、昔の教育に戻った。この研究を続けてきて、私は今私たちがやるべきことはいたずらに新しいものを追うのではなく（もちろん、全面否定しているのではない）、古き日本の先人が残した教育実践を研究し直し、現在の私たちがやっていない（気がついていない）過去の優れた教育実践を伝承発展していくことだと考える。確かに、ＩＴ化がさけばれる中、戦後や古くは大正時代とは学校が取り巻かれた状況は大きく異なる。
だから、大昔の実践をそのまま実施することは無理があるだろう。『数学基礎』も確かに『数学一般』のリバイバルではあるが、今風にアレンジされている。ただ、そのアレンジによって、また『面白くない数学』になってしまっているのではないか。カビ臭い大昔の教科書を読めば読む程、モチベーションが高かったであろう大昔の教師たちの奮闘ぶりが浮かんでくる私である。
さて、次章では、もっと具体的に『数の表記法』についてふれられている別の教科書の一部を紹介したいと思う。
数学のはじまり
§１ 数学はどんな必要から生まれたか。
大昔の人たちは、鳥やけものをとったり、魚をとったりしながら、木の陰に寝たり、岩穴に泊まったりして生活していた。この人たちも獲物を数えたり、仲間の人数を調べる必要があったであろう。しかし、生活が進んで、一定の土地に住んで農業をするようになり、また、人々が集まって群落を作り、社会生活をするようになると、いっそう数学が必要になってくることは、だれにもわかることである。生活が進めば数学が必要になり、数学を用いればますます生活が向上する。これは、私たちの生活を反省してみてもうなづける。
古くから進んだ生活をし、文明の源としてよく知られているのは、エジプト・バビロニア・インド・中国などである。そこには、いずれも大きな川に沿って肥えた平野があり、人々はそこで農業を中心とした生活を営み、いずれも紀元前３０００年ごろから一つの国を作っていた。
これらの国では、人々は毎日の生活のほかに、国の事業として、用水や排水の設備、耕地の整理などの土木工事、宮殿や神殿などの建築をしていた。このような大きな事業を計画し、それをなしとげたり、そのために必要な費用をまかなったりすることは数学の力をかりないでできるだろうか。分業が発達するにつれて、取引も盛んになり、また、農耕の季節を正確に知るために、天文観測なども行われるようになった。このような必要から数学が生れ、数学の発達と文明の進歩とが互に助け合ってきたのである。
人々の住居が定まり、大ぜいの人が共同して生活するようになると、個人の生活を安定させるためにも、社会の平和と秩序を保ち、正義を守るためにも、いろいろな測定や計算が必要になってくる。このようにして、エジプトでもバビロニアでも数学が生れ、計量や計算の方法がだんだん進歩してきた。１０進法による数え方（エジプト）、６０進法による数え方（バビロニア）、大きな数の計算、分数の考え方、長方形・三角形・円などの面積を求めることなど、あまり完全ではないが、実際に使えるまでにくふうされていた。
ピラミッドはたくさんあって、建造されたのは紀元前２９００年ごろから１９００年ごろの間である。その最大のものは、底辺２３３ｍ、高さ１４７ｍの正四角すいで縦横の角は、水平面に対して正確に５２°になっている。これを造るには、延べ７億人の労力が必要であったろうと推測されている。
（ｂ）測量は、どのように研究されてきたか
ユークリッドによって代表されるギリシアの学問の進め方は、理論を重んずる余り応用を卑しいものとし、実際の生活から離れて行く傾向を生みだした。このユークリッドの頃から、文明の中心はギリシア半島を離れ、アレクサンドル大王の建設したエジプトの新しい都市アレクサンドリアに移った。そして、ギリシアの文化に、更にバビロニアその他の文化を合わせて、新しい文化を作り出したのである。
バビロニアの進んだ天文学を取り入れたアレクサンドリアでは、天文観測の方法が進歩し、それにつれて、図形の実際的な応用として三角比の研究が盛んになった。はじめて、地球の大きさを測ったエラトステネス（紀元前２７５−１９４年ごろ）、地球からの月と太陽までの距離の比を計算したアリスタルコス（紀元前３１０−２３０年頃）、月と地球との距離を計算し、三角比を考え出したヒッパルコス（紀元前１６１−１２６年ごろ）などは、このような研究を進めて行ったおもな人人である。測量の進歩と共に、航海がいっそう安全にできるようになり、文明が次第に広く世界に行きわたるようになってきた。
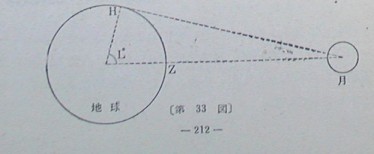ヒッパルコスの測定の原理
次の図は、ヒッパルコスの測定の原理を説明したものである。ヒッパルコスは、地球上Ｚでは月が真上にあって、Ｚとは同緯度でＬ度だけ西によった地点Ｈでは月が水平線上に上がろうとしている時、そのＬを測るとほぼ８９°であることから月と地球の距離を求めた。
●●● 数についての研究は、どのように進歩してきたか。
数についての研究を、数字、数式の表し方、計算の●●●に分けて、その進歩の跡をたずねてみよう。
（ａ）数字は、どのように進歩してきたか。
私たちは、１，２，３，４，５，６，７，８，９，０の１０個の数字を使って、どんな大きな数でも自由に簡単に書き表すことができる。このような便利な数の表し方も、昔からあったのではない。
エジプトでは、すでに１０進法で数えていたが、数を書き表すには、一けたごとに違った記号を用いて表していた。このような方法を用いていると、記録する数がだんだんと大きくなるにつれて、次々と新しい記号を使わなければならなくなり、簡単に数を書き表すことができなくなってくる。
私たちの用いている数字や数の書き表わし方は、インドではじめて考え出され、１２世紀になって、アラビア人がヨーロッパに伝えたものである。ヨーロッパでは、そのころ商業や交通が盛んになろうとしていた。そして、商取引にも航海にも計算を必要としていたので、このインドの記数法は、次第にヨーロッパ全体にひろがって行ったのである。
【考察】
『数の表記法』の比較をするために、昨年夏の撮影時から用意していたデジカメ写真の画像ファイルから原稿として起こしたのがこの第２章の部分である。第１章同様、教材の扱い方（アプローチの仕方）は明らかに『数学基礎』とは異なる。ところで、原稿に起こしつつ内容的な点で一つ気がついたことがある。それは、『神聖文字』をめぐる記述の中で、今回参考にした『数学基礎』の教科書では１０５（通称、おたまじゃくし）止まりであったが、私の前レポートでふれたように１０６（通称、神）を表すものがあることはインターネットで容易にダウンロードできたサイトで確認できたが、さらにその上の位を表すものもあることが挿入されている写真から読みとれる。『それでは、さらにその上の位を表す神聖文字はないのか』こういう些細な（あるいは、くだらない）疑問から学習は発達し、楽しさを増すのではないか。昔と異なり、今はインターネットもあるし、メールでこういったことを研究している大学の先生に直接質問を送信することもできる。些細な実践でよいから教科書の内容から発展した取り組みを工夫していきたいものである。そして、生徒にこうした『あれっ』『はてな』という素朴な感情が積極にわき起こるような教育こそが、画一化した面白くない数学教育を楽しい考える数学教育に変えていくことにつながるのではないか。ただ、目を現実に戻せば、大学に進みたいと言う生徒がいるし、課外講習を強く望む父母の姿や地域の声がある。大学受験に関係のないことではあるものの、こうした『学問に対する好奇心』を育成することは、大学に入って専門的分野の研究を始めるにあたって高校時代に身につけておく最も大切なことなのではないか。いつものことながら夢と現実のギャップに悩まされながら、本章を閉じることとする。