折り紙の特徴は対称性にありますが、その特性を使うことによって、折り紙を一本引く中にも様々な数理があること、2次元から立体が構成されていく過程の諸法則等を体験することができます。
私の知り得る範囲でも折り紙を素材とする幾何教育の実践は多くの方々によって20数年の時を経て豊富な内容を持つものになっています。
このレポートで取り上げたことがらは中学校の学習内容と重なり合いますが、今後の幾何教育のあり方を考える問題提起に少しでもなればと思います。
折り紙が幾何教育に取り入れられる発端となったのは、それまでの伝承の折り紙に対してその折り線に注目したことでした。折り線の法則性に注目しその一般化を考えた堀井洋子氏の実践はあまりにも有名です。1
折り紙は曲線が筈手ですが、その実践に触発されて2次曲線を包絡線で表現する実践も生まれました。また、直接教育には関係しませんが、宇宙科学にも折り紙は応用され、太陽電池パネルに「ミウラ折り」2が使われました。これは一般的な地図等の折り方は直交2方向について順次行いますが、平面を直交2方向同時に一様に折りたたむ方法でした。パネルには特有の規則正しい平行四辺形のパターンが見られます。
出来あがりの作品を想像してください。
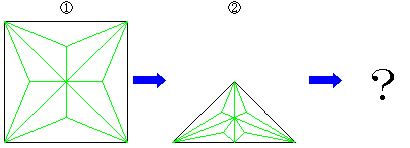
次の①は伝承折りの鶴の折り図ですが、この折り線の構造を②のように直角二等辺三角形に持ち込むとどうなるでしょうか。

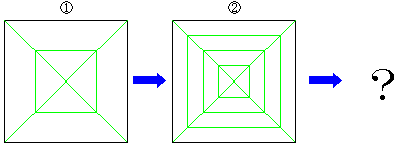
また、次の図の①は同じく伝承の帆掛け舟の折り線図ですが、②のようにさらに折り線を加えます。(山折り谷折りを交互に) 同様にさらにできるだけ多くの折り線をつけ折りあげてゆっくり開くとどうなるでしょう。(これは私にとっては最近の発見です。)
注1 折り紙と幾何 数学教育 1976.3月号-1976.12月