| ① | ② | ③ |
 |  |  |
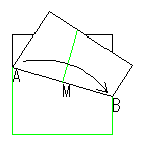| AとBを合わせ AMとBMを重ねる |
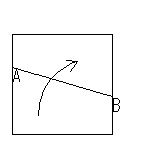
(1)与えられた線分の垂直2等分線をつくること．などがありますが、折り紙では、次のようになります．
(2)与えられた角の2等分線をつくること．
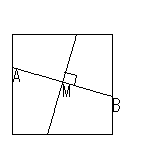
(3)与えられた直線外(上)の点から、この直線に垂線をひくこと．
(1)与えられた線分の垂直2等分線をつくること．
| ① | ② | ③ |
| | |
| AとBを合わせ AMとBMを重ねる |
(2)与えられた角の2等分線をつくること．
| ① | ② | |
 |  | |
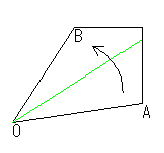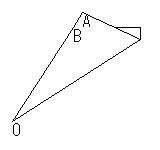| OAとOBを合わせる |
(3)与えられた直線外(上)の点から、この直線に垂線をひくこと．
| ① | ② | ③ |
 |  |  |
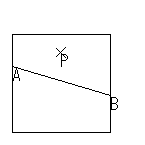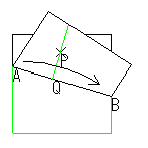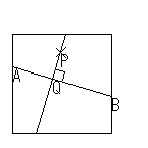| AQとBQが重なる ようにPQを折る |
このことは、辺や角の2等分が簡単にできること、これを繰り返すことによって、折り紙では1/2rが作図可能なことが分かります。
基礎練習として、三角形の5心を折ってみましょう。コンパスを使うより、正確に3直線が1点で交わるのが分かります。
意外と知られていないようですので、ここで紹介しておきます。(この事柄を幾何教育にそのまま持ち込むことについては異論もあるかと思いますが、モデルの作成等には極めて有効な手段となります)
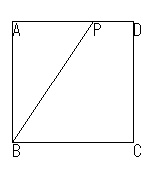
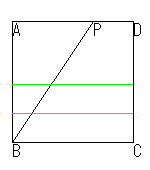
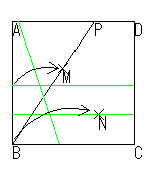
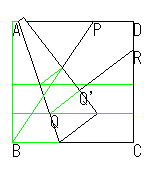
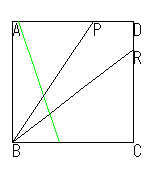
| ① 頂点Bを通り任意の角と∠PBCを作ります。 | ② 適当な幅で折り上げBCに平行な2直線を折ります。 | ③ 図のように2点を移動します。(ここが特徴です) |
 |  |  |
| ④ 紙にたるみがないようにしてきちっと合わせます。 | ⑤ QQ'を延長して、折り目QRをつけます。 | ⑥ ⑤でつけた線を延長して折り目をつけると、∠PBRが求める角です。 |
 |  |  |
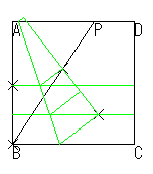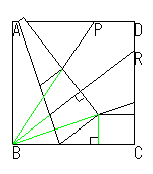右図でBを頂点とする三角形が合同であることから、∠PBCが三等分されることが分かります。
このことによって、例えば正9角形を作成することができることになります。
60°を3等分することによって20°が導かれます。
正9角形の一つの内角は140°ですが、180°-20°×2より、角140°を得ることができるからです。
また、角の2等分を繰り返すことによって、5°単位程度の角も得ることができます。(折り紙分度器が作れる)
理屈の上では、1度単位の角も折れることになります。
以上のような折り紙の特性を理解しておくことが、数学に折り紙を教育に導入する際に大切なことになると思います。
以下の章で、折り紙のもつ数理構造と折り紙による数学的デル(立体)について述べていくことにします。
注3 サイエンス 1980.10月号別冊付録 おりがみの科学