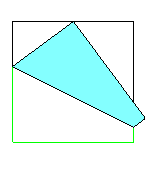
 芳賀の第一定理
芳賀の第一定理正方形の一辺の中点にその辺に含まれない頂点を合わせて折ると、一辺が他の辺の一辺を三等分する。
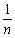 の面積をもつ正方形を折り出すことをテーマに話を進めたいと思います。
の面積をもつ正方形を折り出すことをテーマに話を進めたいと思います。そのために、まず辺のn等分について考えることにします。このことについてはどうしてもオリガミクス45で有名な「芳賀の定理6」について触れる必要があります。(この定理は折り紙の世界にも大きな影響を及ぼしました。私自身もこの定理により長年の課題が解決したものがあります)
 芳賀の第一定理
芳賀の第一定理正方形の一辺の中点にその辺に含まれない頂点を合わせて折ると、一辺が他の辺の一辺を三等分する。 |
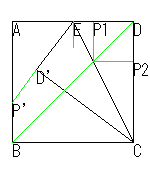
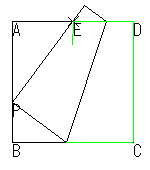
折り紙の辺を三等分する方法は、私の知る限りでは他に次の5つがあります。(図中、②、③では点Eは辺のニ等分点、④、⑤では四等分点を示し、P,P',P1,P2が三等分点です。)
②、③は芳賀の第2,第3定理ですが、②には2つの方法が含まれています。
| ② | ③ | ④ | ⑤ |
 |  |
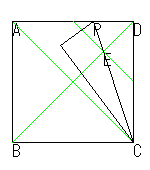 |  |
②について少し説明をします。
P'が芳賀の第2定理で、ABを三等分しますが、よく知られているように折り線ECと対角線BDは互いに他を三等分することよりAD,DCを同時に三等分する点が得られます。これは従来からも折り紙でもよく用いられていたものです。参考までに次ページにこの証明を折り紙のやり方で行ったものを紹介します。
これらはすべて点Eを二等分点だけではなく様々な値を与えることによって一般化が可能になります。しかし、芳賀の第一定理が優れているのは折り方の手数が少なく、しかも多くの数理を含んでいることにあります。
以下にこの芳賀の第一定理の拡張を考えてみることにします。
|
2等分線と比に関する定理
頂角2等分線に沿って3角形を折る.辺Bは辺Aに重なることになる.点Bは点B'に移る.BB'は2等分線CMに垂直であって、このBB'に関して再び3角形片を折ると、MはM'に移る.
折り紙幾何学(伏見康治・満枝著)より
|
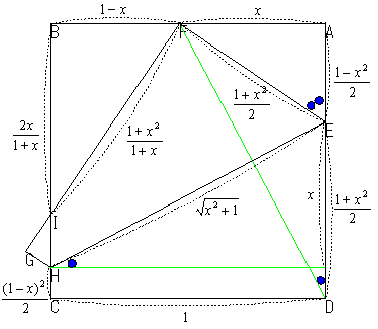
IH=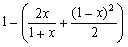
IG=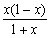
GH=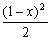
△AEFについて
x2+AE2=EF2
AE+EF=1
これから、AE=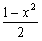 が得られ、△AEF∽△BFIより
が得られ、△AEF∽△BFIより
IB=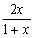
そこで、特にx=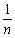 (nは整数)のときは、
(nは整数)のときは、
IB=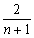
つまり、x=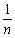 が得られると、
が得られると、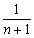 が得られることになります。
が得られることになります。
すでに、n=2の場合は芳賀の定理によりIC=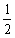 BI=
BI=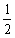 が分かっていますから、これを繰り返すと求める
が分かっていますから、これを繰り返すと求める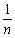 が原理的に求められることになります。実際には、n=2rと先の①〜⑤の中で最も有効なものを利用します。
が原理的に求められることになります。実際には、n=2rと先の①〜⑤の中で最も有効なものを利用します。
これで、辺のn等分が可能なことが分かりました。実際に具体的な数値で考えてみることを薦めます。
次に、いよいよ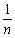 の正方形の作図こなるわけですが、芳賀の定理に関わるいくつかについて寄り道をすることにします。
の正方形の作図こなるわけですが、芳賀の定理に関わるいくつかについて寄り道をすることにします。
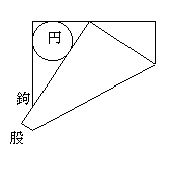 (1) 福島県黒岩虚空蔵堂の算学(明二六)
(1) 福島県黒岩虚空蔵堂の算学(明二六)
今有如図、折方紙作鉤股、容円、只云、
|
この問題は、Sangakuu Theoremとして英文の数学雑誌に掲載されエレガントな解答が募集されたそうです。(1994年)7
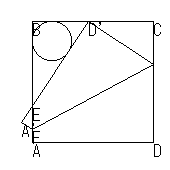 算学定理
算学定理正方形の紙ABCDを図のように頂点Dが辺BC上にくるように折り曲げる。このとき、移動した辺A'D'とABとの交点をEとする。D'がどこにあっても三角形EBD'の内接円の半径はA'Eに等しいことを示せ。 |
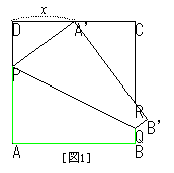 1辺の長さが1の正方形の折り紙ABCDがある。図1のように点Aが辺CD上にくるように折る。折り目となる直線が辺ADと交わる点をP、辺BCと交わる点をQとする。
1辺の長さが1の正方形の折り紙ABCDがある。図1のように点Aが辺CD上にくるように折る。折り目となる直線が辺ADと交わる点をP、辺BCと交わる点をQとする。このとき点AがA'に、点BがB'に移るとする。また、辺A'B'がBCと交わる点をRとする。辺A'Dの長さをxとするとき、次の各間いに答えよ。
(1)辺DPの長さをxを用いて表せ。 98 東京農工大
|
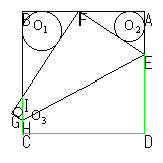 芳賀折りより導かれるもの
芳賀折りより導かれるもの芳賀折りを検討する中で、次のような事柄が導かれました。
(1)AF=x,内接円01,02,03の半径をそれぞれr1,r2,r3とすると、 |
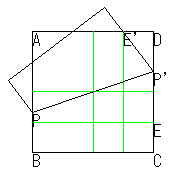
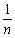 の面積の正方形をつくることができます.(n>1)
の面積の正方形をつくることができます.(n>1)
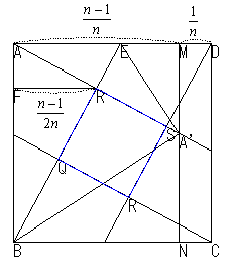
そこで、Bを固定してAがMN上にくるように折り線BEをつけます.
同様に他の3頂点も折ります.すると中に正方形PQRSができます.この正方形の面積はもとの正方形の面積の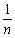 になります.
になります.
MD=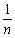 ,AM=
,AM=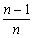 ,PはAA'の中点だから
,PはAA'の中点だから
PF=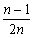
△APBの面積
=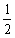 AB×PF
AB×PF
=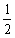 ×1×
×1×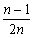
=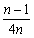
正方形PQRSの面積
=正方形ABCDの面積-4×△APBの面積
=1-4×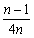 =
=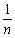
なお、この折り方そのものは「芳賀の第2定理」ですので、求める大きさが「芳賀の第2定理」の拡張で定まる位置A'のときは、前段を省略(MNを折る必要はない)することができます。
例えば、1/5の面積を求めるときは、EがADの中点であるとき、A'の位置からMD=1/5となっているので、直接折りこめることになります。また、nは必ずしも整数である必要はありません。
注4 数学教育 1995.8月号-1996.3月号 ORIGAMICS おりがみを使った新しい課題学習注5 教学教育 1997.9月号- ORIGAMICS II おりがみを使った新しい裸題学習