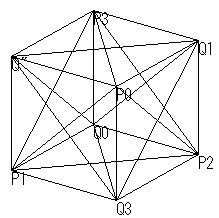空間に次の8個の点P0(a，a，a)，P1(a，-a，-a)，P2(-a，a，-a)，P3(-a，-a，a)， Q0(-a，-a，-a)，Q1(-a，a，a)，Q2(a，-a，a)，Q3(a，a，-a) が与えられている（a>0）． このとき、これらの8個の点を頂点とする立方体をAとする．また、P0，P1，P2，P3を頂点とする正四面体をBとし、Q0，Q1，Q2，Q3を頂点とする正四面体をCとする． 以下の問いに答えよ。 (1)A，B，C それぞれの体積 V(A)，V(B)，V(C)をaで表せ。 (2)B，Cの交わりである立体B∩Cは正多面体である．そのすべての頂点の座標を求め、その正多面体の名称をのべよ． (3)B∩Cの体積V(B∩C)をaで表わせ。 (4)B，Cの結びである立体B∪Cの体積V(B∪C)をaで表わせ。 |
問題そのものの包含関係のモデルを折り紙で作成してみました。
極めて単純な、モデルを見ながら考えると、中学生でも解ける問題だと思いますが、困難さを感じる生徒が多いのが現状だと思います。
私は、これまで以下のようなユニットを使用して、いろいろな多面体を作成してきました。一つは45°ユニットと呼ばれるもので、主に立方体などの作成に使用します。もう一つは60°ユニットと呼ばれるもので、他の正多面体や準正多面体、星形多面体等の作成に使用します。(今回は作品等は省略します。)
ところが、12面体や双対多面体の複合多面体の作成には中々名案が見つかりませんでした。
作成に光が見えたのはやはり「芳賀折り」でした。すぐさま折り紙作家が「芳賀折り」をもとに12面体作成のユニットを考案するところとなりました。
これで、残す課題は次節で紹介する複合多面体となりました。
(1) 45°ユニット
| ① | ② | ③ |
 |  |  |
| 中に折り込む | ||
| ④ | ⑤ | ⑥ |
 |  | |
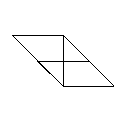| 三角形の部分を 中に折り込む |
(2) 60°ユニット
| ① | ② | ③ |
 |  |  |
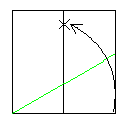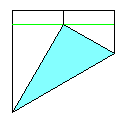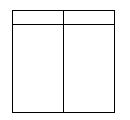| 実数部分を切る | ||
| ④ | ⑤ | ⑥ |
 |  |  |
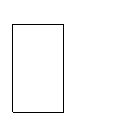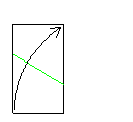| 1：√3の長方形 | ⑤⑥のように折りいったん開いて⑦⑧のように折ります ⑤では逆の折り方があります（他の2頂点を合わせる） | |
| ⑦ | ⑧ | ⑨ |
 |  |  |
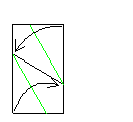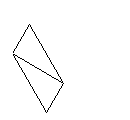| 三角形の部分を中に折りこみます | ||
5つの正多面体のうち、正四面体の双対多面体は自分自身ですから、これは当初から星形多面体として作成できましたし、12面体と20面体の複合多面体ユニット(60枚で作ります)。
正六面体と正ハ面体の複合多面体も組み込みが弱いながらも作成することができました。(最近折り紙作家が折りこみのしっかりしたものを発表されました)
残すのは正12面体と正20面体の複合多面体でした。
正五角形の作図についてはそれまでも色々な案が出されていましたが、誤差が大きかった(ユニットでは致命的なこと)り、正確だが、辺から始まる手数の多いものだったりで実用的でありませんでした。
| ① | ② | |
 |  |
|
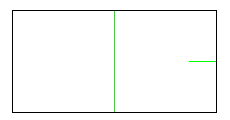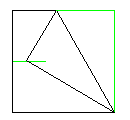| 正方形の半分 | 半分に折り | |
| ③ | ④ | |
 |  |
|
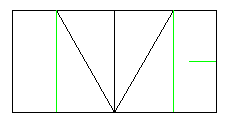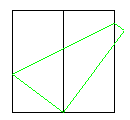| 一度開いて | 芳賀折り | |
| ⑤ | ⑥ | ⑦ |
 |  |  |
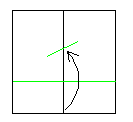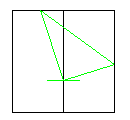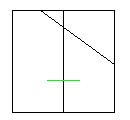| 印をつける | ||
| ⑧ | ⑨ | ⑩ |
 |  |  |
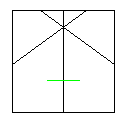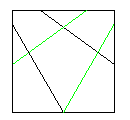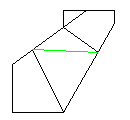| しっかり折る | ひっくり返す 裏の線どおりに中折り | 点線の部分を折る |
| ⑪ | ⑫ | |
 |  | |
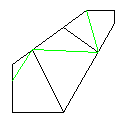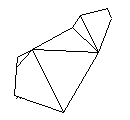| 点線の部分を折る | ||
ところが、1985年の数学セミナー誌上に芳賀折りを利用した極めて穣差の少ない正五角形の作品が紹介され、それをヒントに、108°に対して107.94525323°という精度の高い角を簡単に折り出すことができました。これによってこの複合多面体が作成可能となったわけです。ここでその数理を説明する余裕はありませんが、折り図と作品だけ紹介します。
ここではオイラーの定理、デカルトの定理(凸多面体の各頂点の尖度の和ま720°)等は既知とします。
ユニットを使用してデルタ面体を作成する上で、必要な次のことをまず示します。
デルタ面体の中で、凸多面体の面の数は、4以上20以下の偶数である。
面の数をM，辺の数をHとし、頂点の数Tを、3つの辺が集まっている頂点(3次の頂点と呼ぶことにします。以下同じ)の数T3、4つの辺が集まっている頂点の数T4、5つの辺が集まっている頂点の数T5に分けると，1つの頂点に6つの辺が集まることはないから， オイラーの定理より
M-H+(T3+T4+T5)=2……①
また，1つの頂点を2つの辺が共有するから
2H=3T3+4T4+5T5……②
面は全て正三角形だから，
2H=3M……③
③の左辺は偶数だから、Mは偶数でなくてはなりません。……④
①，②，③より
3M-2(T4+2T5)=12
T4+2T5≧0より 3M≧l2
よって M≧4……⑤
また，①，②，③より
M+2(2T3+T4)=20……⑥
2T3+T4≧0より M≦20……⑦
④，⑤，⑦より Mは4以上20以下の偶数です。
これによって、2面で構成されるユニットが使用可能であることになります。
次に、デカルトの定理より
360°・(T3+T4+T5)-180°・M=720°
つまり、2(T3+T4+T5)-M=4……⑧
⑥，⑧より
3T3+2T4+T5=12……⑨
作成の手がかりとするために、⑨の解をもとめ、具体的に、頂点の一覧表を作ってみます。
| M | T3 | T4 | T5 |
|---|---|---|---|
| 4 | 4 | 0 | 0 |
| 6 | 2 | 3 | 0 |
| 8 | 0 | 6 | 0 |
| 8* | 2 | 2 | 2 |
| 10 | 0 | 5 | 2 |
| 12 | 0 | 4 | 4 |
| 12* | 2 | 0 | 6 |
| 14 | 0 | 3 | 6 |
| 16 | 0 | 2 | 8 |
| 18* | 0 | 1 | 10 |
| 20 | 0 | 0 | 12 |
すると、上の表のようになりますが、*印のついたデルタ凸多面体は存在しません。
上の ⑨式では不充分なのが分かります。式だけでは説明できない空間的な関係があるのではないかと思います。
そこで、実際に作成しながら考えることが必要になります。
まず、5次と3次の頂点は隣り合わないことがわかります。それは、正4面体の辺の中点を通る平面で切り取ると先に紹介したように正ハ面体ができますから、正八面体の2面角と正4面体の2面角は補角ををなしています。したがって、凸多面体である以上これは起こり得ません。実際に条件に合うように作成すると（T3，T5の値が奇数の場合はすべてこの条件にあてはまるので、上の表からは除いてあります）、「8*」は凹んだデルタ8面体、「12*」は平行6面体になってしまいます。
問題は「18*」です。
4面体から順次2面を付け加えていく処方で、16面体から18面体をつくることを考えてみます。それには、外科医の手術のように、下図のように2頂点間を切り開いて、平行四辺形を埋め込むことを考えます。
| ① | ② |
 |  |
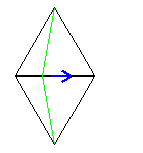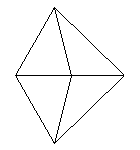16面体を①のように切り開き、そこへ二面を埋め込み②のようにできればよいわけです。ところが、16面体は4次の頂点が2個、5次の頂点が8個有りますが、4次の頂点がはなればなれで相対した位置にあるのです。そのため、どうしても5次の頂点のところに埋め込まざるを得ません。すると、そこは平面になってしまい凸18面体にはなりません。
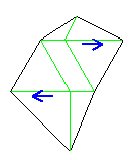
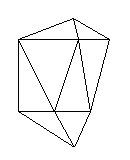
20面体はさらに下図①のように大きく切り開き4面を埋め込むとよいのです。この部分に関しては、トポロジーを用いた方法の考察が高橋鋼一氏によってなされています。8
| ① | ② |
 |  |
以上で、デルタ凸多面体をすべて作成できたことになります。
順にデルタ4，6，8，10，12，14，16，20面体
同時に、位相幾何学の教材化を進める必要も感じます。多面体の理論だけでなく位相幾何学の発展過程で扱われた一筆書きや4色問題等の興味ある題材も多いのです。この問題については過去にも大山斉先生9が提案されてます。
注8 デルタ18面体の非存在について 数学教室1995.9～11