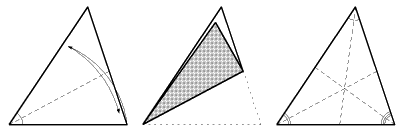
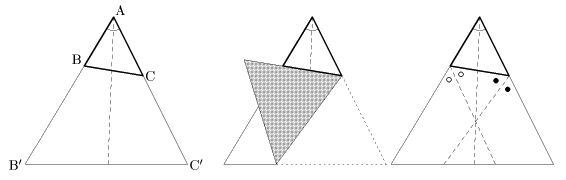
下図の△ABCについて、この内心Iを頂点としてひとつの辺に山折り線IDを引くように三角形を折りたたみます。するとこの山折り線は内心Iから辺BCにおろした垂線になっています。
他の2辺へも同じことを繰り返すと、３つの垂線はぴたりと重なり、下図右のように三角形の3つの辺もきれいに１直線上に重なっていることが分かります。
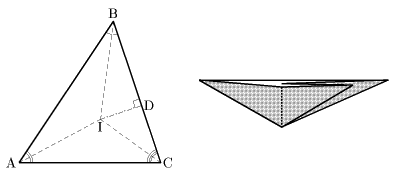
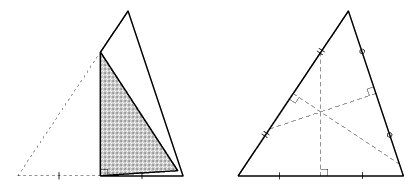
問 上の△ABCについて、AD-AC=DB-DC が成り立つことを右の図で説明しましょう。（AD>ACとします）
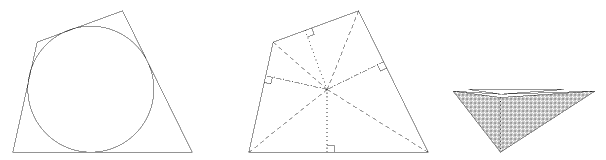
問 下図のように内接円をもつ四辺形も三角形と同様に、４つの辺をそろえて折りたためることを確かめましょう。また、上の問いを参考に4辺の間に成り立つ関係を考えてみましょう。
|
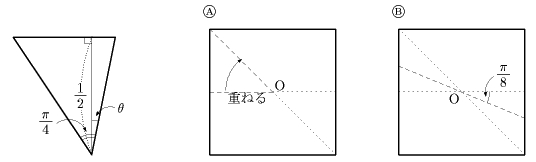
入試問題より(2) 一辺の長さが1の正方形の紙を1本の線分に沿って折り曲げたとき二重になる部分の多角形をPとする。Pが線対称な五角形となるように折るとき、Pの面積の最小値を求めよ． 東京工業大 2001 |
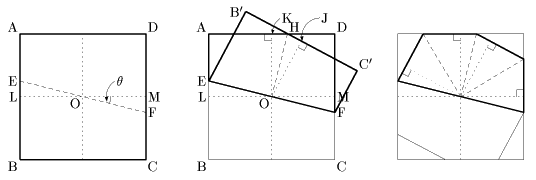
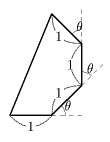
この多角形の二重になった部分を開くと8角形となり、対称性を考慮に入れると、この8角形は正方形の内接円を共有すること（つまり上図でOは正方形の中心＝解答としてはこのことをまず示す必要があるのだろう＝）から8つの合同な三角形（下図左）としてその辺をそろえてたたむことができる。したがって、問題はこの三角形の面積の最小値を求めることに置き換えられる。解としてはθ=π/8,つまり、正8角形になる場合であるが、このことから正8角形の簡単な作図法が導かれる。（下図A、B、以下、上の図のように折る）
入試問題より(2)b[同大では過去にも以下のような問題が出題されている。] 右図のような４辺の長さ1で、それらのなす外角がθ(0<θ<π/2)であるような五角形の面積の最大値を求めよ. 東京工業大 1995 |
問 次のような四角形の場合、４辺を同じ直線上にそろえて折ることができるでしょうか。
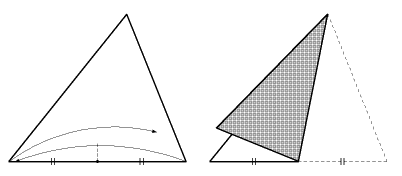
問 この交点から3辺への距離が等しいことを下図のように折ることで確かめてみましょう。また、BH+CH'=BC であることを説明してください。
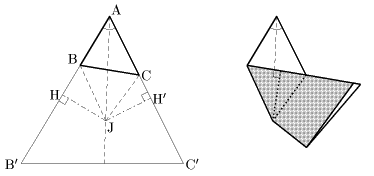
問 次に下図のように、この交点を包み込み３つの頂点が重なるように折り線通りにたたみこの交点と３つの頂点との距離が等しいことを確かめ、その理由を説明してください。
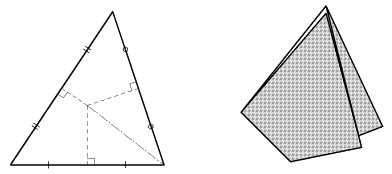
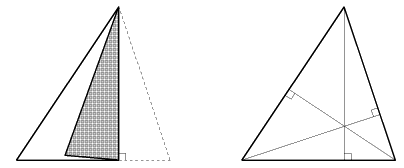
問 重心を折り、この点は中線を２：１の比に分けることを確かめてください。