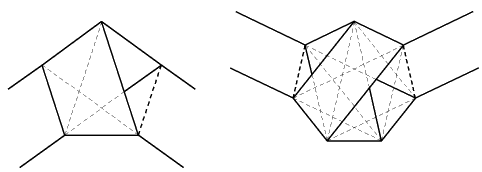

 問 次のことを証明せよ。
問 次のことを証明せよ。
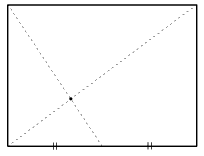
 問 左図のように点線で折るだけで、点・は縦横を同時に3等分していることを証明せよ。
問 左図のように点線で折るだけで、点・は縦横を同時に3等分していることを証明せよ。
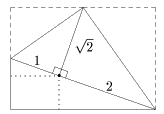 前の2つよりこちらのほうが証明が難しいかもしれない。しかし、折り紙による説明は難しくない。
前の2つよりこちらのほうが証明が難しいかもしれない。しかし、折り紙による説明は難しくない。
右図のように左から折って合わせてみると、二つの直角三角形は相似であり相似比は√2:1である。
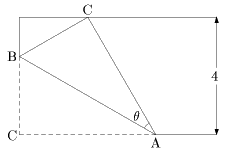 入試問題より(3)
入試問題より(3)右の図のように幅4のテープの端点Cが対辺に重なるように折るとき、三角形ABCの面積が最小になるようなθとそのときの面積を求めよ。 名古屋大 1999 |
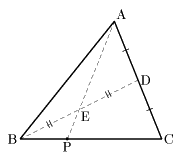
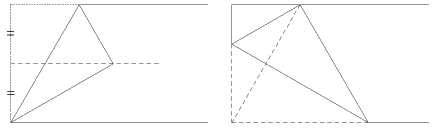
問 上記の問題において、θ=30°のとき△ABCの面積は最小になるが、このとき点Bはテープの幅の3等分点となっている。では実際にこの作図はどうしたらいいだろうか。その作図法は以下の図の通りである 。このことを説明せよ。
| 数樂コーナー |
※<紙テープで遊ぼう>
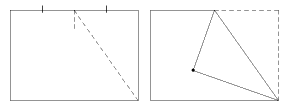
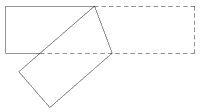 問 長方形の紙を右の図のように折ると、重なる部分が三角形を作る。この三角形は二等辺三角形であることを証明せよ。(問題集:数研4STEP 数学Aより)
問 長方形の紙を右の図のように折ると、重なる部分が三角形を作る。この三角形は二等辺三角形であることを証明せよ。(問題集:数研4STEP 数学Aより)
問 上の問題で、重なった部分の三角形の面積が最小になるのはどのように折ったときか。
問 上の問題で、重なった部分が正三角形となるようにしたい。その作図法(折り方)を考えてみよう。
問 テープをくぐらせて結んで、正5角形・正7角形を作ってみよう。