丂惓擇廫柺懱偼20屄偺崌摨側惓嶰妏宍傪柺偲偡傞懡柺懱偱丄偦偺12屄偺捀揰偼1偮偺媴乮奜愙媴乯忋偵偁傞乮塃恾嶲徠乯丏惓擇廫柺懱偼奜愙媴偺拞怱偵娭偟偰懳徧側恾宍偱偁傞丏
丂堦曈偺挿偝偑1偺惓擇廫柺懱偺1偮偺曈傪AB偲偟丄偦偺曈偺拞揰傪M偲偡傞丏偝傜偵丄奜愙媴偺拞怱傪O偲偡傞丏
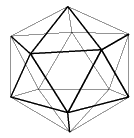 丂3揰A,B,O傪捠傞暯柺偱偙偺惓擇廫柺懱傪愗偭偨偲偒丄愗傝岥偲偟偰摼傜傟傞榋妏宍偺捀揰傪弴偵A,B,C,D,E,F偲偡傞丏偙偺偲偒丄C,F偼偙偺惓擇廫柺懱偺曈偺拞揰偱偁傝丄3偮偺慄暘OM,OC,OF偺挿偝偼摍偟偄丏師偺奺栤偄偵摎偊傛丏
丂3揰A,B,O傪捠傞暯柺偱偙偺惓擇廫柺懱傪愗偭偨偲偒丄愗傝岥偲偟偰摼傜傟傞榋妏宍偺捀揰傪弴偵A,B,C,D,E,F偲偡傞丏偙偺偲偒丄C,F偼偙偺惓擇廫柺懱偺曈偺拞揰偱偁傝丄3偮偺慄暘OM,OC,OF偺挿偝偼摍偟偄丏師偺奺栤偄偵摎偊傛丏
- 慄暘 OM 偺挿偝x傪媮傔傛丏
- 奜愙媴偺敿宎傪l偲偡傞偲偒丄l2傪媮傔傛丏
- 兛,兝傪偙偺惓擇廫柺懱偺1偮偺曈傪偼偝傫偱椬傝崌偆2偮偺柺偲偡傞丏O 偐傜兛,兝偵壓傠偟偨悅慄偺懌傪偦傟偧傟G,H偲偡傞偲丄偦傟傜偼奺柺偺廳怱偱偁傞丏兤=佢GOH偲偡傞偲偒丄sin 兤/2偍傛傃cos兤傪媮傔傛丏
嶳宍戝丂2001
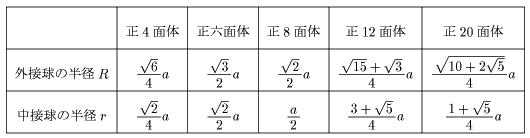
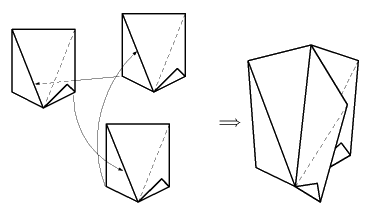
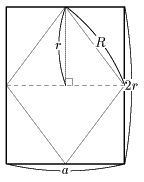 丂塃恾偺傛偆側梡巻偐傜儐僯僢僩傪嶌惉偟傑偡丅廲墶偺戝偒偝偼忋偺昞傪嶲徠偟偰偔偩偝偄丅R偼奜愙媴偺敿宎丄倰偼拞愙媴偺敿宎傪昞偟傑偡丅
丂塃恾偺傛偆側梡巻偐傜儐僯僢僩傪嶌惉偟傑偡丅廲墶偺戝偒偝偼忋偺昞傪嶲徠偟偰偔偩偝偄丅R偼奜愙媴偺敿宎丄倰偼拞愙媴偺敿宎傪昞偟傑偡丅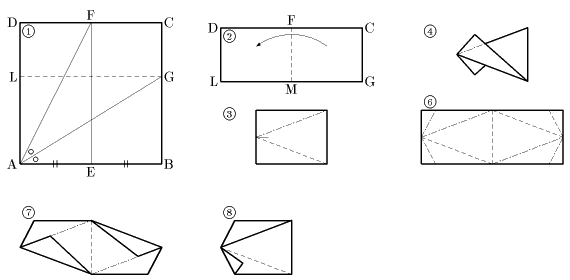
 丂
丂 丂
丂