 のパッケージ,作図例はemathP 等のパッケージを利用しています.
のパッケージ,作図例はemathP 等のパッケージを利用しています.
 のパッケージ,作図例はemathP 等のパッケージを利用しています.
のパッケージ,作図例はemathP 等のパッケージを利用しています.
|
%\documentclass[a4paper]{jarticle} %\title{Complex operator による図形変換\\ %{\normalsize$\cdots\cdots$ 反転と方ベキの定理による一次変換のアプローチ}} %\author{札幌新川高等学校 中村文則 } %\begin{document} %\maketitle %実際はこの下の\begin{center}〜\end{center}を削除、上の%をとる% \begin{center} {\LARGE Complex operator による図形変換}\\[4mm] {\normalsize$\cdots\cdots$ 反転と方ベキの定理による一次変換のアプローチ}\\[6mm] {\large 札幌新川高等学校 中村文則 }\\[5mm] \end{center}
\item [\textit{Chap.1}]{\bf 作用素としてのアプローチ}\par
|

|
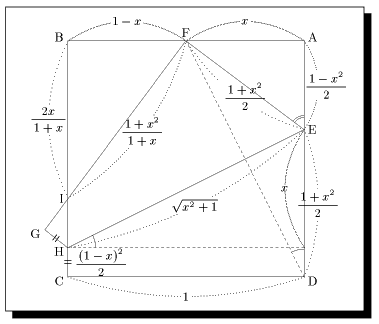
\unitlength0.22cm\small% \begin{picture}(30,30)(-5,-3)% \def\C{(0,0)}% \def\B{(0,24)}% \def\D{(24,0)}% \def\A{(24,24)}% \def\F{(12,24)}% \def\E{(24,15)}% \def\H{(0,3)}% \def\I{(0,8)}% \Suisen\H\F\I\G% \Suisen\H\A\D\J% \Hen_ko[80]<0.7>\H\E{$\sqrt{x^2+1}$}% \Hen_ko[40]<0.5>\E\A{$ \ \ \ \ \bunsuu{1-x^2}{2}$}% \Hen_ko[70]<0.7>\I\F{$ \bunsuu{1+x^2}{1+x}$}% \Hen_ko[40]<0.5>\D\E{$ \bunsuu{1+x^2}{2}$}% \Hen_ko[40]<0.9>\C\H{$ \ \ \ \ \bunsuu{(1-x)^2}{2}$}% \Hen_ko[40]<0.7>\B\I{$ \bunsuu{2x}{1+x}$}% \Hen_ko[80]<0.7>\A\F{$x$}% \Hen_ko[80]<0.7>\F\B{$1-x$}% \Hen_ko[80]<0.7>\C\D{$1$}% \Hen_ko[80]<0.7>\E\J{$x$}% \Hen_ko[40]<0.5>\F\E{$ \ \ \ \ \bunsuu{1+x^2}{2}$}% \Dashline[50]{0.3}{\F\D}% \Dashline[50]{0.3}{\H\J}% \Drawline{\H\E\F\G\H}% \KAKUkigou\J\H\E[2]{\makebox(0,0)[l]}% \KAKUkigou\A\D\F[2]{\makebox(0,0)[l]}% \KAKUkigou<2>\A\E\F{\makebox(0,0)[l]}% \Touhenkigou<2>\G\H% \Touhenkigou<2>\C\H% \Put\A(1mm,1mm)[l]{A}% \Put\B(-1mm,1mm)[r]{B}% \Put\C(-1mm,-1mm)[r]{C}% \Put\D(1mm,-1mm)[l]{D}% \Put\F(0,1mm)[b]{F}% \Put\E(1mm,0)[l]{E}% \Put\H(-1mm,-1mm)[r]{H}% \Put\I(-1mm,0)[r]{I}% \Put\G(-1mm,-1mm)[r]{G}% \Drawline{\C\D\A\B\C}% \end{picture}% |
|
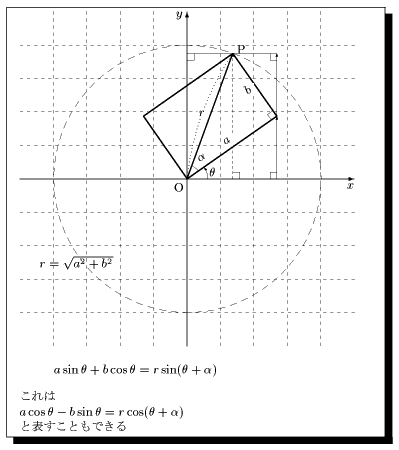
\unitlength8.5mm\small \begin{zahyou}(-5,5)(-5,5)% \def\O{(0,0)} \def\A{(4,0)}% \def\B{(0,4)}% \zahyouMemori[g][n]% \Put{(0,0)}{% \Daenko[0.5][0.5]{4}{4}{0}{360}}% \kyokuTyoku(4,70)\P% \Put\P(0,1mm)[l]{ P}% \kyokuTyoku(4,35)\R% \kyokuTyoku(4,125)\S% \thicklines% \Drawline{\O\P}\Suisen\P\O\R\H% \Drawline{\P\H}\Suisen\P\O\S\L% \Drawline{\P\L}\Drawline{\L\O\H}% \thinlines% \Suisen\P\O\B\U \Suisen\H\O\A\V% \Suisen\H\U\P\Y \Suisen\P\O\A\X% \ArrowLine\H\Y \ArrowLine\V\H% \ArrowDashLine[60]{0.1}\X\P% \Drawline{\U\Y}% \KAKUkigou\H\O\P{% \makebox(0,0.5)[l]{% \rotatebox{35}{$\alpha$}}}% \KAKUkigou[a]\A\O\R[1.5]{% \makebox(0,0)[l]{$\theta$}}% \Hen_ko[40]<0.3>\P\O{$r$}% \Hen_ko[0]<0.3>\H\O{% \rotatebox{35}{$a$}}% \Hen_ko[0]<0.3>\P\H{% \rotatebox{35}{$b$}}% \Tyokkaku\H\O \Tyokkaku\X\P% \Tyokkaku\Y\V \Tyokkaku\V\X% \Tyokkaku\U\Y% \Put{(-3.3,-2.5)}(0,0){% $r=\sqrt{a^2+b^2}$}% \end{zahyou} \[a\sin \theta+b\cos \theta=% r\sin(\theta+\alpha)\] これは\\ $a\cos \theta-b\sin \theta% =r\cos(\theta+\alpha)$\\ と表すこともできる |