前節のベクトルの例に比べると,その定義はわかりにくいものになっている.いま筆者が使っている教科書7)では次のようにベクトルを定義している.
向きを指定された線分を有向線分という.有向線分AA'において,Aをその始点,A'をその終点という.また線分AA'の長さを,有向線分AA'の大きさ,または長さという.有向線分の位置を問題にしないで,その向きと大きさだけを考えたとき.この有向線分をベクトルという.したがって,下の図のように.位置が違うが,向きが同じで長さが等しい有向線分ABとCDは,ベクトルとしては,同じものを表す.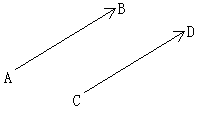 (中略).1つのべクトルを有向線分をもちいて表わすとき,その始点は平面のどの点にとってもよい.有向線分PQで表されるベクトルを, 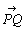 と書き表す.また,ベクトルは,一つの文字と矢印を用いて, と書き表す.また,ベクトルは,一つの文字と矢印を用いて, のようにも表される.(中略) のようにも表される.(中略)2つのベクトル  , ,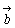 が等しいとは が等しいとは , ,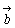 の向きが同じで,大きさが等しいことである.このことを の向きが同じで,大きさが等しいことである.このことを = =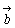 で表す.ゆえに で表す.ゆえに = =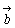 ならは,それらを表す有向線分を平行移動して,重ね合わせるこのこともできる.また,このことの逆も成り立つ. ならは,それらを表す有向線分を平行移動して,重ね合わせるこのこともできる.また,このことの逆も成り立つ.
|
ていねいに説明してあるが,よくわからない部分もある.ここでは3つの記号が登場する.①有向線分PQ,②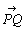 ,③
,③ である.説明から①と②は異なった概念であることが強調されるが,有向線分を表す記号が導入されていないので.どうもすっきりとしない.また②と③の関連がよくわからない?.ほとんどの生徒は①②③を区別しないで使っているような気がする.
である.説明から①と②は異なった概念であることが強調されるが,有向線分を表す記号が導入されていないので.どうもすっきりとしない.また②と③の関連がよくわからない?.ほとんどの生徒は①②③を区別しないで使っているような気がする.
ベクトルの定義をめぐる種種の混乱は,有向線分PQと有向線分PQによって表されるベクトル との混同から生じているのではないかと思う.幾何学的べクトルのあまりに厳密すぎる定義は,また別の意味でわからなくなる原因ともなるが,ここでは文献3)からベクトルの定義の部分を多少長くなるが引用してみよう(ただし,簡単のため2次元の場合に限定し,記号や表現を少し変えてある).
2次元Euclid空間R2においてベクトルaは向きづけられた成分(有向教分)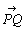 で表わされる.ただし,2組の有向成分 で表わされる.ただし,2組の有向成分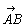 と と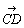 において, において,(*) 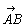 と と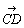 が同じ向きで,線分としての長さが等しいとき, が同じ向きで,線分としての長さが等しいとき,またこのときに限り, 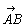 と と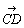 とは同一のベクトルaを表すものと考える.従ってR2内の有向線分の集合を考え,(*)によって同値関係 とは同一のベクトルaを表すものと考える.従ってR2内の有向線分の集合を考え,(*)によって同値関係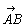 ~ ~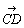 を定義するとき,各同値類をR2におけるベクトルと呼ぶことができる.この意味で今後ベクトルを[ を定義するとき,各同値類をR2におけるベクトルと呼ぶことができる.この意味で今後ベクトルを[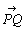 ]またはその代表をとって単に ]またはその代表をとって単に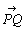 と表す.有向線分 と表す.有向線分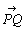 の始点P,終点Qを,ベクトル の始点P,終点Qを,ベクトル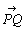 の始点,終点ということもある. の始点,終点ということもある.
|
一読して,同値類の箇所を除けば,高校教科書よりすっきりとした感じを受けるであろう.その原因は,各有効線分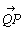 と有向線分の集合(同値類)[
と有向線分の集合(同値類)[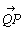 ]の記号をきちんと区別していることである.同値類の説明をていねいにすれば,高校生にとっても後者のほうがわかり易いのではないかと思う.そして,後でベクトルの成分表示を説明するときにも,同値な有効線分が表すベクトルの成分が一致することも極く自然に理解される.
]の記号をきちんと区別していることである.同値類の説明をていねいにすれば,高校生にとっても後者のほうがわかり易いのではないかと思う.そして,後でベクトルの成分表示を説明するときにも,同値な有効線分が表すベクトルの成分が一致することも極く自然に理解される.
次にベクトルの和とスカラー倍がどう定義されているか見てみよう.まず高校教科書7)では,
2つのベクトル , ,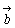 があるとき,1点Oを任意に定めて があるとき,1点Oを任意に定めて = =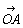 となる点A,Cをとり,ベクトル となる点A,Cをとり,ベクトル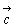 = =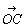 を考える.この を考える.この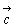 を を , ,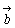 の和といい, の和といい,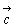 = = + +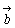 で表す. で表す.すなわち, 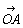 + +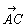 = =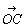 この定義は点Oのとりかたに無関係である.(中略). この定義は点Oのとりかたに無関係である.(中略).一般に,ベクトル  と実数kに対し,積k と実数kに対し,積k を次のように定める. を次のように定める.[1]  ≠ ≠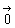 ,k≠0のとき ,k≠0のときk>0の場合 大きさが│  │のk倍で,向きが │のk倍で,向きが と同じであるベクトル と同じであるベクトルk<0の場合 大きさが│  │のk倍で.向きが │のk倍で.向きが と反対であるベクトル と反対であるベクトル[2]  = =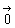 またはk=0のときは,k またはk=0のときは,k =0 =0すなわちk 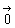 = =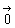 ,0 ,0 = =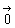 上の定義から(-k)  =-k =-k ,特に (-1) ,特に (-1) =- =- である. である.
|
次に文献3)では以下のように定義している.
ベクトルa=[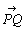 ]に対して,2点P,Qの定める直線上に点Rをとり,RがPからQへ向かう半直線上のときは+を,そうでないときは-をとることにして, ]に対して,2点P,Qの定める直線上に点Rをとり,RがPからQへ向かう半直線上のときは+を,そうでないときは-をとることにして,λ=±│PR│/│PQ│ とおき,ベクトルb=[ 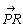 ]をb=λaと表わす.ただし,│PR│,│PQ│は線分PR,PQの長さである.ベクトルλaをベクトルaのスカラー倍という.(中略). ]をb=λaと表わす.ただし,│PR│,│PQ│は線分PR,PQの長さである.ベクトルλaをベクトルaのスカラー倍という.(中略).ベクトルa=[ 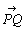 ],b=[ ],b=[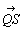 ]とするとき,ベクトルc=[ ]とするとき,ベクトルc=[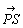 ]をc=a+bと表して,aとbとの和という.特にO=[ ]をc=a+bと表して,aとbとの和という.特にO=[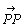 」を零べクトル(ゼロベクトル)といい,a=[ 」を零べクトル(ゼロベクトル)といい,a=[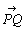 ]に対して-a=[ ]に対して-a=[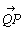 ]と定める. ]と定める.
|
どちらの定義も基本的には同じである.そして,両者ともこのあと上で定義したベクトルのスカラー倍と和がベクトル空間の8つの公理を満たしていることが示されている.
上のベクトルの定義と全く異なる定義をしているのが三省堂の教科書6)である.三省堂の教科書ではベクトルをまず最初に数ベクトルとして定義している.一部省略して引用する.
|
物音に驚き,魚がいっせいに同じ向きに動くことがある.
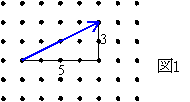 図1のような移動は,途中の経路を無視すると,1目盛りを1として右へ5,上へ3動いたのだから(5,3)と数の祖で表すことができる.点のこのような移動を変位という.(中略) 変位と同様に,数の組みで表すと都合のよい量に力や速度などがある.このような量をベクトル量といい,ベクトル量を表す実敦の組をベクトルという.ベクトルを1つの文字で表すときは,  , ,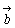 などと書く. などと書く.2つのベクトル  =(a1,a2), =(a1,a2),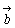 =(b1,b2)があり,a1=b1 かつ a2=b2 のとき. =(b1,b2)があり,a1=b1 かつ a2=b2 のとき. と と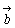 は等しいといい, は等しいといい, = =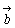 と書く. と書く.ベクトル  =(3,2)を,変位を表すのに使った矢線を用いて,下のように図示したとき,ベクトルの矢線表示という. =(3,2)を,変位を表すのに使った矢線を用いて,下のように図示したとき,ベクトルの矢線表示という.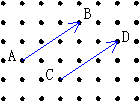 そして,Aを始点,Bを終点といい,aを 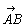 とも書く.始点をC,終点をDとして とも書く.始点をC,終点をDとして は は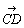 とも書ける.すなわち とも書ける.すなわち  = =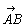 = =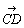 である.また,ベクトル(3,2)の3や2を成分といい,この表し方を,ベクトルの成分表示という. である.また,ベクトル(3,2)の3や2を成分といい,この表し方を,ベクトルの成分表示という.
|
力や速度などをベクトル量と呼ぶことは後で示すように難点があるが,ベクトルの定義に関しては,前の2つに比べるとすっきりしている.なお,本文では,ベクトルの成分表示を,
(3,2) または 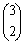
のように,座標形式と列ベクトルとを併用しているが,いまの議論に関係しないので,列ベクトルの部分は省略してある.ベクトルの和とスカラー倍の定義は次のようになっている.
|
ベクトル(4,2)で表される変位と(-1,3)で表される変位を続けて行うと,ベクトル(3,5)で表される変位となる.また,(4,2)で表される力と(-1,3)で表される力を合成すると(3,5)で表される力となることが知られている.
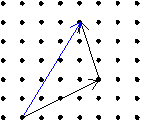 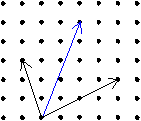 このようなベクトル量の性質を表すため,2つのベクトル  =(a1,a2), =(a1,a2),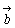 =(b1,b2)の和 =(b1,b2)の和  + +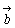 を次のように定める. を次のように定める.(a1,a2)+(b1,b2)=(a1+b1,a2+b2). (中略) 実数kとベクトル  =(a1,a2)について =(a1,a2)について のk倍すなわちk のk倍すなわちk を次のように定める. を次のように定める.k(a1,a2)=(ka1,ka2) たとえば,  =(1,2)のとき,2 =(1,2)のとき,2 =(2,4)となり,矢線表示では,aと同じ向きに2倍の長さとなる.また,-2 =(2,4)となり,矢線表示では,aと同じ向きに2倍の長さとなる.また,-2 =(-2,-4)であるから,-2 =(-2,-4)であるから,-2 は は と逆向きに2倍の長さとなる.このようにk と逆向きに2倍の長さとなる.このようにk は,k>0のときはaと同じ向き,k<0のときはaと逆向きになる.またk=0のときは は,k>0のときはaと同じ向き,k<0のときはaと逆向きになる.またk=0のときは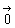 である. である.
|
最初からベクトルを数ベクトルとして定義してあるので,説明がたいへんに簡潔になっている(前節の[例1]を参照).前の2つの記述にくらべると,三省堂の教科責の方が生徒にとってわかり易いのではないかと思う.何よりもこの教科書の良いところは,読んでいて面白いことである.