物理や工学においてはベクトル(数学における)とベクトル量(自然科学における)の区別はやや曖昧である.例えば岩波理化学辞典では速度の定義を次のように述べている9).
[速度] 運動する点の変位の時間に対する割合で,時間tの関数としての位置ベクトルr(t)の導関教v=dr/dtで与えられるベクトルである。(中略) vの大きさ 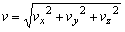 を速さという。方向はrの描く曲線の接線方向を向く。 を速さという。方向はrの描く曲線の接線方向を向く。
|
これらのベクトル量は前節の幾何学的ベクトルと基本的な点で異なっている.その第1は平行移動が可能かそうでないかの違いである.幾何学的ベクトルを失印(または有効線分)で表したとき,その矢印を平行移動してもベクトルとしては同じものであった(むしろ,平行移動しても変わらないものとしてベクトルを定義したのであった).そのことを強調するために,幾何学的ベクトルを自由ベクトルということもある.これに対し,速度や力,変位などは平面内のどの点におけるベクトル量なのかを指定しないと意味がない.具体的には矢印の始点Pを決めてやればよい.
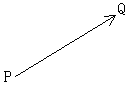 a=[
a=[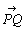 ]
]自由ベクトルに対し,このようなベクトル量は点Pにおける束縛ベクトルと呼ばれている.いいかえると,束縛ベクトルとは平面内の点Pとaを合わせたものである.
相違点の第2はベクトルの和に関してである.幾何学的ベクトルでは,離れた2つの始点をもつ矢印を自由にたすことができた.ところが力のベクトルに関しては,始点(正唯には力が作用する点)が異なれはそれらの和も一般的に異なる.例えば,下の図のように2つの力f1とf2を合成した結果は(a)と(b)とでは異なっている.(注:いまの場合f1,f2は剛体にはたらく力を表している)
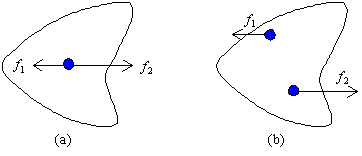
速度の場合には,同じ始点をもつ速度ベクトルどうしでないとそもそも和を考えることができない.速度の合成や分解は平面上の各点ごとに定義されるものである.しかも,同じ始点をもつ速度ベクトルであっても,任意の2つの速度の和がいつでも定義できるとはかぎらない.例えば,2つの異なった質量m1とm2をもつ質点どうしをくっつけると質量m1+m2をもつ質点ができあがるが,2つの異なった速度v1とv2をもつ質点どうしをくっつけることなどまったくできないからである(この違いは遠山啓らによって,外延量と内包量という量の区別によるものであると指摘された8)).一般に,速度の和は一様に流れる川のなかを進む船の場合のように限定された状況のなかで定義されるものである.
変位ベクトルでは,最初の矢印の終点と,後の矢印の始点がー致する場合でないと和が定義できない.
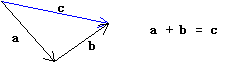
上の図において,移動aに続けて移動bを行えば結局は変位cで表される移動となる.これをa+b=cとかけば変位ベクトルの和が定義できる.ところが,変位の始点が固定されていると,b+aという和を定義することはできない.つまり変位ベクトルの和では交換法則が成立しないのである(森毅は加法を分解し,このような和を添加と呼んでいる10)).
つまり,大きさと向きをもった量をベクトルと定義すると,これらは必ずしも数学的なべクトルの公理系をすべて満たさないのである.初学者にとってベクトルの概念が分かりにくい理由はこのあたりにあるのであろう.
高校生にベクトルをどう指導すればよいかということについては,様々な考え方があるところである11).筆者の経験からいうと,ベクトルの概念を高校生にきちんと区別させるには,数学におけるベクトルと物理など自然科学におけるベクトル量とをある段階できちんと区別して教える必要があると感じている.そのためにはベクトル場という概念を新たに導入し,ベクトルとベクトル場の違いを鮮明にした方がよいのではないかと考えている.そこで次節でベクトル場について説明しよう.