ニュートン以降の力学の研究からベクトル場の考えが芽生えてきた．オイラーやラグランジュなどによる解析力学および微分方程式の研究とともに発展してきた．歴史的にはベクトルとベクトル場の概念はほぼ同時期に認識されたといわれている．
物理学では，ある物理量が空間や時空の関数として表されるとき，これを場（ば）と呼ぶ習わしがある（英語ではfieldと綴る）．また振動数やエネルギーの関数として表されるとき，スペクトルと呼んでいる（英語ではspectrum）12) ．その物理量がベクトル量である場合，つまり空間の各点からベクトル量への対応をベクトル場（vector field）と呼ぶ（もし物理量がスカラー量ならスカラー場という）．実際そのようなべクトル場は物理の中にたくさん存在する．例えば，力学における力の場や速度場，電磁気学における電場や磁場，量子力学における量子場などがその代表例である．つまり，物理に登場するほとんどのベクトル量は実はベクトルではなくベクトル場なのである．
数学ではベクトル場とスカラー場（2次元ユークリッド空間R2の場合）を次のように定義している．
|
[ベクトル場・スカラー場の定義]3) R2 内のある集合D上で定義されたスカラー値の関教をスカラー場(scalar field)，べクトル値の関教をベクトル場(vector field)，ベクトル場はその成分の関数の性質に応じて，連続，微分可能などの性質を定義する． |
具体例をいくつかあげておこう．
[例1]カの場(fieid of force)
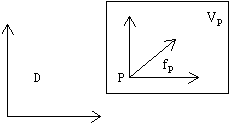
平面内の領域Dの1点Pに作用する力を，Pを始点とする矢印fPで表す．力の作用する向きは矢印の向きと等しく，力の大きさは矢印の長さに比例している．ここで注意しなければならないのは，幾何学的な矢印の長さは力の大きさとは無関係であることである(幾何学的ベクトルでは，矢印の長さ=ベクトルfpの大きさであった．力の大きさはN(ニュートン)という単位で測られる)．前節で示したように，点Pに作用する力fPはスカラー倍と和が考えられるのでfPはベクトルとなる．言い携えると，点Pに作用する力全体の集合VPは，数学的概念としてはベクトル空間としてとらえられるのである．
D内の任意の点Pに対し上のような力fPが存在すれば対応：P→fPが考えられる．
これをDを定義域とする力の場と呼ぶ．イメージ的には平面内の各点Pにパソコンのウィンドウズ画面のように別の平面VPをべ夕べ夕と貼り付けたようなものである．
[例2]速度場(field of velocity)
平面内の領域Dの中を運動する点を考え，その軌跡がなめらかな曲線Cによって表されているとする．Cは時間tをパラメーター（助変数）として(x(t)，y(t))と表すことができる．
ここでx(t)，y(t)はtの微分可能な関教であり，導関数
vx=dx/dt，vy=dy/dt
が存在する．これをv=(vx，vy)とかく．t=t0を固定するとv(t0)は時刻t0におけるこの点の速度を表す．vはtのベクトル値関数であるが，tの値を1つ指定すると，Cの場所が1つ決まる（簡単のため曲線Cは自分自身と交わることはないとする）．したがって，vはCを定義域とするベクトル値関数と考えることができる．これをC上の速度場と呼ぶ．幾何学的にはvは曲線Cに対する接線方向のベクトルである（接ベクトルとも呼ばれる）．
[例3]行列によって定義されるベクトル場5)13)
2×2行列Aを
とする．2次元ユークリッド空間R2の原点を適当に定め，その位置ベクトルを
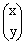と書く．Aの位置ベクトルに対する線形作用（1次変換）を
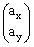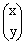
=によって定義すると，
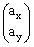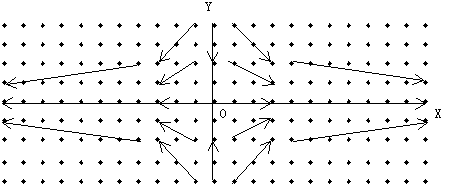
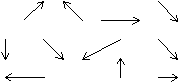
はベクトル場となる．これを行列Aによって定義されるべクトル場という．例えば，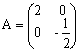
によって定義されるベクトル場は下のような流れを表わす．