x(t)を実変数tの微分可能な関数とし,dx/dtをその導関数とする.いま,もっとも単純な微分方程式
dx/dt=ax (aは実定数) (1)
を考える.この微分方程式は,高校程度の数学の知識があれは簡単に解くことができる.そのために(1)を変数分離して,
dx/x=adt
と書きなおし,両辺を0からtまで(xについてはx0からxまで)定積分する.結果は,
log x-log x0=at
log x/x0=at
となる.ここでlogは自然対数である。x/xo =eat となるので,
x(t)=x0 eat
が解である.ここでeは自然対数の底,x0=x(0)である.x0は初期値と呼ばれることもある.
次に.2変数x(t),y(t)に関する微分方程式の系,
dx/dt=a1x
dy/dt=a2y (2)
を考える(a1,a2 は実定数である).(2)の解は(1)と同様にして,
x(t)=x0exp(a1t)
y(t)=y0exp(a2t)
となる.ただし.x0,y0は微分方程式系(2)の初期値x0=x(0),y0=y(0)である.さて(2)をベクトルの記法を使って書き換えてみよう.まず関数x,yをR2の点(x,y)だと思うと,ベクトル値関数f(t)=(x(t),y(t))はR2内の(なめらかな)曲線を表す.変数tは時間とみることもできれば.曲線のパラメータ(助変数)とみることもできる.幾何学的にみれば(dx/dt,dy/dt)はこの曲線上の点(x,y)における接線方向を向いているので,ベクトル場
f'(t)=(x'(t),y'(t))
は曲線fの接ベクトル場と呼ばれる.もしtが時間を表せば,f'は速度場である.ここで,2×2行列Aを
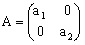
とおけば(2)は
f'=Af
となってたいへん単純なかたちとなる.(3)から線形写像Aは,対応f→f'によってR2上のベクトル場を定義することがわかる.例えば,a1=2,a2=-1/2,すなわち,
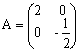
とすると,このベクトル場はちょうど前節の[例3]のような矢印で表されることがわかる.
さて,適当な初期条件のもとで(2)または(3)の微分方程式を解き,それをR2の点としてプロットしていけば,いくつかの曲線群がえられる.それらをスケッチしたものが次の図である.
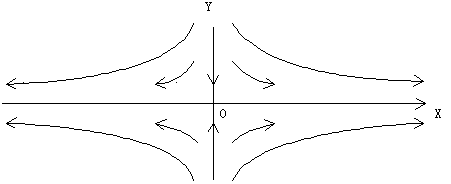
微分方程式を解くということは,幾何学的には,与えられた初期条件のもとで,接ベクトルをつないで曲線f(t)をもとめることである.f(t)を解曲線(積分曲線ともいう)と呼ぶのはこのような理由からである.tを時間とみれば,f(t)はの微分方程式に従って平面R2上を運動する粒子の軌道(orbit)と考えることができる.これらの曲線族の定性的な研究分野のことを現代数学では力学系(dynamical system)と呼んでいる.歴史的には,フランスの数学者ポアンカレによるニュートン力学の3体問題の研究に始まるといわれている.彼は微分方程式を解く代わりに,解のもつ定性的性質(現代風にいえば位相的性質)は何かということを研究したのである.
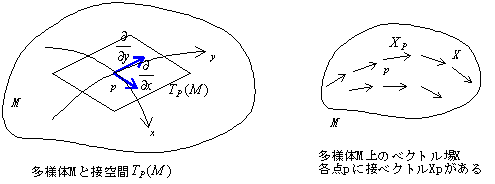
これまでは平面R2上のベクトル場について考えてきたが,さらに一般化してn次元ユークリッド空間Rn内のなめらかな(超)曲面上のベクトル場というものも考えることができる.これは多様体上のベクトル場と呼ばれている.多様体(manifold)とはごく簡単にいえば,なめらかな曲線や曲面の概念を一般化したものである(正式には微分可能多様体といい,ふつうMとかく).数学では、例えば球面のような(曲がった)曲面上で定義されたベクトルを次のように考える.われわれが世界旅行をするとき,平らな平面上を移動するのではなく,実際は曲がった(大きな)球面上を移動する.これと同じように,なめらかな曲面Mの上をなめらかな道に沿って移動している旅行者を想像しよう.各瞬間の旅行者の速度ベクトルを表す矢印Xpは,完全にはM上にはないはずである.始点PだけがM上にあるが,Mが曲がっているために,終点に近づくにつれ,だんだんMから離れていく.速度ベクトルXpを含む平面はある点Pだけで,Mにくっついている.この平面のことを,元の曲面Mに対する接平面といい,TP(M)とかく.先ほど速度ベクトルを接ベクトルと呼んだのはこのような幾何学的な理由からである.
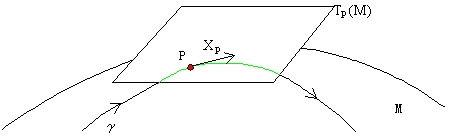
微分幾何では多様体M上のベクトル場を微分の概念をつかって定義する.いままでのベクトルの定義と違うので,Mは2次元の場合(曲面)について簡単に説明する14)15).いまM上の任意の点をPとする.Pの近くの点はこの近傍で定義された局所座標系(x,y)で表すことができ,さらに,Pを通るM上のなめらかな曲線γは5節の例2のように,tというパラメ-タによって,γ=(x(t),y(t))と表される.
さて,fをPの近くで定義されたM上の関教f=f(x,y)とすると,曲線γに沿ったfの点Pにおける微分df/dtというものを考えることができる.つまり詳しく書くと,
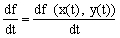
である.幾何学的にはdf/dtはfの曲線γ方向への変化率である.合成関数の微分公式によって上式は
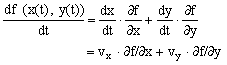
とかける.ここで(vx,vy)は前に出てきた速度ベクトルであるが,今度はMが曲がっているために,平面R2のベクトルとみなすことができない.むしろ,上の式を象徴的に
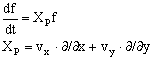
と書いて,fに対する微分作用素Xpを曲線γに沿って運動する速度ベクトルとみなす.Xpは点Pにおける曲線γの接ベクトルと呼ばれる.もっと一般にM上には自由に曲線を描くことができるから,成分が(vx,vy)ではなく,一般の実数の組(ax,ay)であるような接ベクトルXPを考えることができる.歴史的には(ax,ay)を反変ベクトル(の成分)と呼んだ.これに対し(∂/∂x,∂/∂y)は接ベクトルの基底と呼ぶ.M上の点Pにおける接ベクトル全体は2次元のベクトル空間をつくるが,これを接空間(tangento space)と呼びTp(M)とかく.Mの各点Pに対してXpが対応しているとき.
X:P→XP
Mにはベクトル場Xが与えられているという.多様体とベクトル場の関連についてはたいへん興味深いものがあるが,またいずれ別の機会にふれたいと思う.