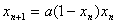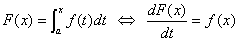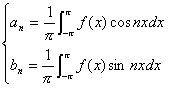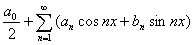北数教第25回数学教育実践研究会数学教育現場における基礎研究について
平成9年度研究報告書
北海道大学理学部科学教育研究室
北海道石狩南高等学校数学科教諭 小 栗 是 徳
*** 目 次 ***- はじめに
- 研究概要
- 研究内容
(1) 発展方程式
(2) カオス
(3) ルベーグ積分
(4) 大学院資格試験の受験
(5) 大学院理学研究科(修士課程)ゼミナール受講
(6)『高校生のための数学講座』受講 - 結語-今後の進展を踏まえてー
- 付録
(1) 発展法方程式要旨
(2) 発展方程式レポート
(3) カオス要旨
(4) カオスレポート
(5) ルベーグ積分の具体例
(6) ルベーグ積分要旨
*お断り*- 5(2)の発展方程式レポートは,久保田教授からの指導を受けた結果のものである。
- 本報告書は,目次のとおりであったが,本研究会のレポート発表のため3(4)の一部と5の付録すべてを大幅に省略した。
|
1.はじめに
(1)科学教育研究室とは何か
科学教育研究室とは,「科学教育研究室実施要領」の通り,小中高の現場の理科教育(算数数学含む)の担当教員に対して,理科教育について基礎的研究を与えることによって,その資質を向上し,その指導力の強化を図ることを目的に設置されたものである。(2)入室に至る経緯について①科目等履修生としての入学 教育職員免許法改正に伴って,従来『経験年数15年以上』によって申請取得できた専修免許が平成6年3月31日をもって経験年数だけでは取得不可能になった。不可能となった教員は,大学院において所定の単位を修得せねばならない。
平成8年10月1日,平成8年度後期北海道大学理学研究科に『科目等履修生』として入学し,次の計10単位を取得した。
| 講座名 | 担当教官 | 開講形式 | 内容 | 評価 |
|---|
代数学考究1
(4単位) | | 大学院資格試験 | 線型代数学 | B合格 |
解析学考究1
(4単位) | | 大学院資格試験 | 微分積分学 | B合格 |
非線型偏微分方程式
(2単位) | 儀我美一教授 | 講義 | 幾何学的発展方程式 | A合格 |
この中の大学院資格試験については,3(5)で後述する。 非線型偏微分方程式では,幾何学的発展方程式を中心に,4階微分方程式で記述される問題から始まって,最適制御の問題をきっかけに発展した粘性解の理論と等高面の方法の最近の進展までを扱うものであった。事前に,担当の儀我教授からは予備知識は不要と聞いていたが,実際,始まってみると代数学・幾何学・解析学の基礎をもとに展開し,特に関数解析学との関連が深かった。学生時代に関数解析学を履修しなかった私は,ついて行くのが大変であった。特に,最後のレポート問題の提出には一カ月がかりであった。大学院生にアドバイスをもらいながら5問中3問半解答し,A合格であった。
正直なところ,はじまる前は果たしてついていけるかどうかという不安をもち,いざはじまってみるとわからないことだらけで絶望感をもち続けていた。落ちこぼれ生徒の境遇である。しかし,終わってみると,確かに難解ではあったが,既に完成されたものでなく,研究途上ものを学んだという充足感があった。
②科学教育研究室への入室
平成9年3月,『科目等履修生』を終了するにあたって,わずか半年では物足りなさを感じた。引き続いて研究を続ける方法について探ったところ,この科学教育研究室を知った。儀我教授をはじめ数学教室及び職場の上司である学校長の快諾も得られ,入室することができた。
(3)入室の目的次の2点にある。- 数学教師としての専門性を高める。
- 数学教師としての指導力を強化する。
では専門性とは何か,またそれをどう高めたか,更に指導力をどう強化したかについての具体的内容を以下の通り報告したい。
2.研究概要
(1) 研究期間平成9年5月1日~10年3月31日
(2) 研究日時毎週2回(火曜・金曜)13:00~18:30
(3) 研究場所北海道大学理学部数学教室
(4) 指導教官久保田幸次教授(専門は偏微分方程式,関数解析学)
但,『カオス』のみ津田一郎教授(専門は複雑系カオス,脳理論)
(5) 研究概要一覧
| テーマ | 担当教官 | 主な研究内容 | 開講形式 | 備考(テキスト等) |
|---|
| 発展方程式 | 久保田幸次教授 | 偏微分方程式 | 講義 | 『偏微分方程式論入門』井川満著 |
| カオス | 津田一郎教授 | カオス理論 | 講義 | |
| ルベーグ積分 | 久保田幸次教授 | ルベーグ積分論 | ゼミ | 『ルベーグ積分』溝畑茂著 |
| 修論ゼミ | 久保田幸次教授 | 波動方程式 | ゼミ | |
以下,大学院資格試験
| 試験科目 | 試験内容 | 試験結果 | 備考(参考にしたテキスト等) |
|---|
| 代数学考究1 | 線型代数学 | A合格 | 線型代数学 佐武一郎著
線型代数学 大嶋勝著 |
| 解析学考究1 | 微分積分学 | A合格 | 数学解析上 溝畑茂著
数学序説上下 一松信著 |
| 解析学考究2 | 複素関数論 | B合格 | 工業数学 ワイリー著
関数論演習 辻正次著 |
| 解析学考究3 | ルベーグ積分 | B合格 | ルベーグ積分 溝畑茂著
ルベーグ積分入門 伊藤清三著 |
3.研究内容
(1) 発展方程式
大学院修士課程の学生を対象にした講義で,波動方程式・熱方程式及びラプラス方程式の初等的な取り扱いからはじめ,更に進んだ取り扱いをするため超関数・Sobolev空間の入門をした。 主な講義内容は
1)波動方程式とエネルギー保存則
2)熱方程式と最大値の原理及び軟化子
3)ラプラス方程式の固有値問題
4)超関数の定義と基本的性質
5)急減少関数と緩増加な超関数のフーリエ変換
6)ヒルベルト空間とソボレフ空間入門
講義の要旨は,付録1の通りである。
講義の進め方は非常に丁寧で分かりやすく,分からなければ質問もしやすい雰囲気であった。毎回レポート課題が出されて,すべて提出して指導を受けた。この指導内容も赤ペンで添削指導されており,理解を深めるのには効果的であった。提出結果は,課題21問中,A合格が17問,B合格2問,不合格2問であった。詳しくは,付録2の通りである。また,このレポート課題は,主に微分積分学の復習を兼ねたものなので,後述の大学院資格試験対策にも効果的であった。
(2) カオス 大学院修士課程の学生を対象にした講義で,最近急にわき起こったカオスについて,歴史的背景を踏まえ,カオスの定義,定理を中心にカオス理論の入門をした。 まず,カオスとは何か。どんなものをカオスと呼べるのか。語意からすると,英語では『Choas』をケーオスと発音し,『無秩序,大混乱,混とん』という意味なので,一般にはこの意味で誤解されている。ところが,ギリシャ語ではカーオスと発音し,家から外に出るとなにがあるかわからないという意味で,BC800年ヘシオドスの神統記では『creativevoid(創造的空虚』)という意味で書かれている。数学では,1975年以降,この言葉が用いられた。数学的定義は,付録3に記述した。数学以外の普通の言葉で定義すると『カオスとは,法則(決定論的)でありながら予測しがたい結果(非決定論的)をもたらすもの』ということになる。以下,『カオスとフラクタル』山口昌哉著を参考に,報告する。
1941年,京都大学農学部の昆虫学者,内田俊郎博士は豆につく豆ゾウムシの増殖について観察し,次のロジスティック方程式を得た。
(A)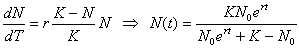 (N:固体数,t:時間,r,K:定数)
(N:固体数,t:時間,r,K:定数)
これに対して,1973年,ロバート・メイは次のように(A)を理論的に再考した。(A)において,近似差分方程式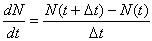 とおくと
とおくと
(B)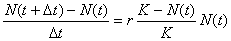
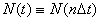 とおくと(B)は
とおくと(B)は
(C)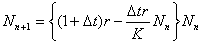
(C)で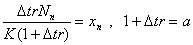 とおくと
とおくと
(*) 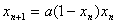
これは,離散力学系,つまり決定論的式である。初期値x0を与えれば(*)によってx1,x2,・・・,xnが次々と求まってくるからである。
a<ac(≒3.75)のとき,初期値x0の取り方に無関係に収束や振動が起こるが,a>acになった途端,(*)という離散力学系の軌道は一変する。ここでは,初期値x0の取り方に依存してあらゆる数の周期をもつ軌道も現れると同時に,いかなる周期ももたないような軌道も現れる。また,初期値x0を少しでも変えると極めてセンシブルに軌道の様子が一変する。acは,critical pointの略である。
ロバート・メイは,これをchoaticと呼んだ。
以上のことは,ポケットコンピューターでも確かめられるので,この例は,カオスを理解するのに,高校生にも分かる好例ともいえる。
離散力学系(*)を一般化したのが,1973年の『リー・ヨークの定理』である。数学界にあって,この定理は極めてざん新であり,当時としては相当ショッキングなできごとであった。実はこの10年前,ローレンツ乱流について研究していたが,数学の壁に阻まれていたところ,たまたまその論文がリーとヨークに手渡されたといういきさつがある。リーとヨークはこの時点では,ロバート・メイの仕事を知らなかったが,二人で『リー・ヨークの定理』が成立するという予想を立てた訳である。数学で,『カオス』と言う言葉が登場したのは,このときが初めてである。
主な講義内容は
1)カオスの定義
2)ローレンツアトラクター
3)アトラクターとアトラクティングセット
4)次元論
5)ホースシューマップ
講義の要旨は,付録3の通りである。
講義の内容は非常に難解で分かりにくかった。参考書も紹介されたが,講義のスピードが速く,参考書の一部をかじっただけで不勉強であったと反省している。レポート課題も3題出されたが,手をつけることができたのはその内の1題だけで,それも前半しかできなかった。詳しくは,付録4の通りである。このレポート課題は,「『リー・ヨークの定理』の定理を証明せよ」というものであった。この課題を出すとき,津田教授は,『この定理は連続関数の基本的性質を使うだけで,学生にもできる』と言っていた。その言葉を信じ,2~3週間に渡って離散力学系(*)を手掛かりに四苦八苦したが,全く先が見えず教授のところに相談にいったところ,「抽象的に考えなければ出ない」といわれ,1973年のリーとヨークの論文の原書を手渡してくれた。『数学英和・和英辞典』を手掛かりに,約1月がかりで漸く前半部分のみ自分のものとして証明できたので,提出した。その内容は,確かに連続関数の基本的性質を使ってはいるが,無限の集合列を使わないとできない部分があり,その発想は私の力をもっては不可能なことであった。
(3) ルベーグ積分 今回の科学教育研究室で,一番の勉強になったのが,このルベーグ積分である。その理由と内容を以下の通り報告する。 学部3年生を対象としたゼミである。前期は,学生3名が交代で教授の指導の下で,黒板に出てテキストの内容を説明した。このときは,私は遠慮してしまい,オブザーバーであった。後期は,学生が2名減って1名になったので,私も学生といっしょに指導を受けた。
教授によるゼミの指導は,徹底していて,いささかのあいまいさも許されなかった。例えば,学生が『明らかに』とやると,『どうして明らかなのか』と指摘されたり,テキストの通り棒読みすると,『そこを説明しなさい。』と指示される。また,図から直観的に明らかなことも必ずと言っていいほど論証を求められた。このような理由を教授は『ルベーグ積分を理解するのに,厳密な論証を怠るとあとでわけがわからなくなる。』と説明していた。
説明は,常に明快さを求められた。明快さをもって説明するためには,説明者自身がよくわかっていなければできない。抽象化の壁に立ち往生していると,『書きなさい』と言われる。教授の助言を借りて,黒板に書くと具体的になり壁を乗り越えることができた。
①ルベーグ積分に至る歴史的経緯について
まずこのことについて,『リーマン積分からルベーグ積分へ』小谷真一著(数学セミナー1997.10)を参考に確認する。
周知の通り,微分積分学は17世紀ニュートン,ライプニッツによって導入された。当時としては偉大なことであったが,現在からみると非常に直観的で厳密性に欠けるものであった。そこで,180年後にリーマンがリーマン積分を定義したのち,ジョルダン・ボレル測度を経て,1902年ルベーグが学位論文『積分・長さ及び面積』を著すに至るまでをたどってみる。
ニュートン,ライプニッツ以来,微分積分学の基本定理
☆ 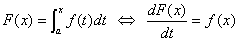
は,どのような関数fについて成立するかという問題が,以後の微分積分学の研究の原点となった。
19世紀初め,コーシーは関数を実数を実数に対応させるものとして,初めて抽象的に考えた。それまで何らかの式で表されるもののみを関数としていた見方から,大きく前進させた。また,連続性という概念を初めてε-δ方式で定義した。しかし,まだ実数の連続性,有界閉集合のコンパクト性等が認識されていなかったので,コーシーのいう連続は,今でいう一様連続であった。
コーシーの同時代のフーリエは,熱伝導の研究からフーリエ級数を考えていた。fを周期2πの関数とし,n∈Zに対して
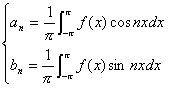
とおく。このとき,フーリエ級数
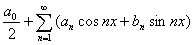
はf(x)に収束するとした。
ところが,どのようなfに対してそのフーリエ級数が元のfに収束するのか,また,同時にR上に拡張した不連続関数に対して積分をどう定義するかという問題が生じた。これを考察したのがリーマンである。
1854年,リーマンは,独自のリーマン和を考えて,リーマン積分を定義した。これによると有界変動関数をはじめ,可算個の不連続点をもつ有界関数まで含めて,積分可能となった。具体例は付録5を参照。
しかし,実数の完備性,一様連続性はまだ明確に認識されておらず,リーマン積分の真の意味の確立は,デデキント,カントール,ワイエルシュトラスまでかかった。
1894年,ジョルダンはRnの有界集合Eに対して,Eを含む有界区間Iについて,Eの特性関数f(x)=CE(x)がIでリーマン積分可能のとき,
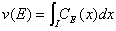
をEの測度と呼んだ。
このRnを抽象化し,一般の集合Sに対して,有限加法性をもつ部分集合族J(S)を考えて,(S,J(S),v)をジョルダン測度空間という。
一方,1898年,ボレルは,Rnの開集合や閉集合に対して完全加法性等の性質をもつ測度mを考えた。mの最大定義域をB(Rn)とすると,これはRnの部分集合族で性質を満たす中で最小のものである
J(S)とB(Rn)との関係は単純でない。このジョルダン測度とボレル測度を統合したのが,ルベーグである。ルベーグは,1902年の学位論文『積分,長さ及び面積』の中で両測度の問題を解決すると同時に,微分積分学のき☆の問題も解決した。ルベーグは,独自のルベーグ測度を導入し,両測度を統合した。このとき,ルベーグ測度の対象となる集合を,ルベーグ可測集合という。次に,このルベーグ可測集合を用いて可測関数を定義し,可測集合の上でルベーグ積分を定義した。
有界可測集合上の有界可測関数は,すべてルベーグ積分可能となる。具体例は付録5の通りである。
②本ゼミについて
ルベーグ積分を理解するのは,ルベーグ自身の著作『積分,長さ及び面積』を読むのよいことはいうまでもない。しかし,同書は,特に初めの測度論が難解であり,初学者の場合そこでつまずいて先に進めないことが多い。そこで,本ゼミでは,それとは異なった展開で書かれたテキストを用いた。本ゼミで使用したテキスト『ルベーグ積分』溝畑茂著は,1952年のリースの考えに負うものであり,ルベーグ積分がリーマン積分の直接的な拡張であることを明快に示す方法である。これによると,まず,微分積分学の基礎となる連続関数についての基本的性質(一様連続性,一様収束等)を確認しながら,リーマン積分に入り,その中でリーマン積分可能な条件をルベーグが零集合を使って言い換えた定理も紹介しながら,可測関数を定義してから,可測集合を定義し,ルベーグ積分を導入するものである。
主な内容は次の通り
1)連続関数の積分
2)収束列,一様収束列
3)リーマン積分の定義,リーマン積分可能な条件
4)リーマン積分の性質
5)リーマン積分可能な関数の性質
6)ルベーグによるリーマン積分可能な関数の特徴づけ
7)可測関数
8)測度的収束,測度的極限
9)可測関数列の基本的性質
10)有界可測関数の積分
11)可測集合
12)Egoroffの定理
13)ルベーグによる積分の定義
14)可測集合上での積分
この中で,特に重要なものを付録6とした。
(4) 大学院資格試験について
これは,大学院理学研究科の中で数学専攻だけが取り入れて実施しているユニークな制度である。これは,「大学院生手引き」の通り,大学院修士課程の学生を対象に,年2回試験を実施して合格すれば4単位を与えるというものである。事前に講義はなく,与えられた試験範囲や参考書をもとに,すべて自学自習よって試験に臨むわけである。合格には,A合格とB合格とがある。資格試験に,5科目合格し,その中に博士課程の教官団が指定した3科目のA合格が含まれていれば,その教官団の中から指導教官を選定し,直ちに博士論文作成の準備に入ることができる。 私は,前記の『科目等履修性』のとき2科目B合格し8単位を取得していた。今回の科学教育研究室にあっては,受験する必要がなかったが,儀我教授の勧めを頂いて,研究の基礎固めのため4科目受験した。その結果は,詳しくは15頁から25頁までの通り,4科目中,2科目がA合格,2科目がB合格であった。特に,A合格については,2~3年がかりのつもりでいたので,予想以上の収穫であった。儀我教授と久保田教授からの指導の成果であったと感謝したい。両教授からも激励され,また自信もついて,研究にも大きな弾みがついた。
(5) 大学院理学研究科(修士課程)ゼミナール受講について
久保田教授の指導する修士論文ゼミナールに,オブザーバーとして参加し指導を受けた。ここでは,3人の修士課程の学生が,3次元の非線形波動方程式の初期値問題を異なった条件のもとで研究し,修士論文を作成していた。内容は,(1)の『発展方程式』との関連性が強く,また微分積分学の復習にもなったので,オブザーバーでありながら積極的に質問して指導を受けた。 この中では,同時に論文作成の手法についても,学ぶことができた。
(6) 『高校生のための数学講座』受講について
北海道大学理学部数学教室では,高校生を対象に夏と春の2回各3日間『高校生のための数学講座』を開講している。石狩南高校の生徒を引率して,高校生と一緒に受講した。大学の先生が,高校生をにわかるようにそれぞれ工夫して教材を提示していたが,私でも分からなかったことが多く,『難しいことを分かりやすく教えること』の困難さを改めて痛感した。- 平成9年8月4日『1で始まる数が多いのはなぜか』吉田知行教授
- 5日『コンピューターに数学研究ができないのはなぜ?』辻下徹教授
- 6日『だ円の弧長とだ円曲線』中村郁教授
- 平成10年3月24日『ランダムな数とカオス』津田一郎教授
- 25日『ベクトル場』諏訪立雄教授
- 27日『フェルマーの夢見たこと』前田芳孝助教授
4.結語-今後の進展を踏まえて-
(1) 社会人としての再教育
大学の専門教育を受けるのは,なんと20年ぶりであった。しかも学部のうえの大学院であったので,難解であった。 社会人として再教育を受けると,学生時代とは違った意味での新鮮さを覚える。まず第1に,社会人であるという以上学生時代のような甘えは許されないということである。第2に,今後の人生を考えたとき大学の専門教育を受けられるのはこれが最後になるかもしれないという切迫感があった。第3に,現場を離れての研修なので,新しい世界との出会いや新しい自己の発見ができたことであった。
(2) 教員の研修
教育公務員特例法に『教育公務員は絶えず研究と修養に努めなければならない』とある。教員の研修について権利と同時に義務を明文化したものである。 ところで,現場においては研修のための研究会は,官民を問わず多彩である。その内容は現場に即したものが多く,まれにそうでないものがあると,『現場に使えない』と総すかんをくってしまう。確かに教育という営みは,理論よりもまず目の前の生徒をどうするかである。実践的な分野が中心であり,その実践の積み重ねこそが教員の研修の命であるといっても過言ではない。しかし,その実践の足元としての基礎研究がおろそかであったら,その実践がいかに優れていようがまさに足元からすくわれてしまうであろう。
数学教育も同じである。目の前の『わからない,できない』生徒をどうするか,わかる生徒にはもっと力をつけさせたい,教材も選び方,その提示の仕方,授業展開,評価等々,どれをとっても今すぐ必要とするものばかりで手が抜けない。これら臨床的研究に追われていて,基礎的研究ができないのが実状である。しかし,臨床的なものは,えてして体系的でなく系統性も欠いて学問的でないことを忘れてはならない。
小学生を教えるには小学校まで,中学生を教えるには中学校まで,高校生を教えるには高校までの知識さえあれば指導上は特に困らない。高校数学の場合,16世紀の微分積分までの内容であるから,教師もそこまで分かっていれば現場で必要としないという理由もここにある。しかし,つい20年前に生まれた『カオス』のように学問としての数学は今も発展している。数学史上は,16世紀までを初等数学・古典数学,17~18世紀を近代数学と,19~20世紀を現代数学という。世界史的にも16世紀まではゆるやかな進歩であったが,ルネサンスを契機に急速に科学技術が進歩し,数学も大きな貢献をした。21世紀が目前に迫った今の生徒を教えるためには,教師自身いくら専門性を高めても高めすぎることはない。
教育の現場は多忙である。とにかく日々の業務に追われて自己研修するための時間的・精神的余裕は皆無に等しい。現場の1人として,私の教員人生を振り返ってもそうである。したがって,充電できないということの不安は常に持っている。特に,数学の専門性における研修不足というのは深刻である。学卒以来,もし基礎研究のないままだとしたら,ひょっとしたら間違ったことを教えているかもしれない。間違ったことを教えてもだれも指摘してくれないのが教育の現場である。あるいは,数学の力を知らず知らずのうちに落としているかもしれない。いずれも数学教師として不名誉なことであり,あってはならないことである。一番の悲劇は,そのような数学教師に教わる生徒の側にある。自分だけはそんなはずはない,といううぬぼれを持ってはならないことも今回の研究によって思い知らされた。
この意味で今回の科学教育研究室は,その目的の達成には十分なものであったと断言できる。
(3) 数学の特性
数学というものは,本当に不思議な学問である。その1つに,『わからない,できない』から『わかる,できる』への不連続性がある。つまり,『わからない,できない』という状態からあるとき突然,『わかる,できる』状態に転移してしまうのである。これはどうしてなのか,その中身はブラックボックスである。その構造は全くわかかってない。とにかく,だれもが一度わかってしまうとそれまで分からなかった自分がまるで別人であるかのようになってしまうのである。また,まだ『わからない,できない』状態でいる他人に教えることは容易とは限らない。それは,自分でも何故『わからない』から『わかる』ようになったのかわからないからである。 数学教師自身も,今目に前にいる生徒同様かつて『わからない,できない』から『わかる,できる』ようになったはずである。ところが,教師を長年続けていると,このことを忘れ生徒が『どうしてわからないのか』『なぜできないのか』と嘆いてしまう。教師自身も1つの研究分野を持つことにより,生徒と同様に,『わからない,できない』という数学を勉強する以上避けることのできない現実を共有することは,教師の目線を下げることにもなる。
大学の理学部の中にあって,数学科は他の分野と比べると,非実験非実習,全く理論的という点で特殊な存在である。つまり,極端にいえば,テキストと筆記具さえあれば,だれでも,どこでも,数学の勉強や研究が可能だということである。また,論理的に正しければ必ず認められる。ここに,数学独自の『自由と平等性』がある。実際,歴史を見ると偉大な数学者たちの中には,独力で研究・開発をやり遂げてきた人達がいる。
しかし,私の場合,今回の科学教育研究室をふりかえって独力で勉強・研究することの困難さを痛感した。例えば,『ルベーグ積分』のゼミでは,1回のゼミのために事前に10時間くらいの準備をして,自分では完ぺきのつもりでゼミに臨んだところ,久保田教授の指摘で詰めの甘いところがボロボロとほころびてきて,ゼミの後それを修正してまとめるのに5時間位かかったということが多かった。自分では本当に情けなくなる思いであったが,久保田教授から『自分ではできないからここにきて指導を受けているわけです』といわれ,うなづいた次第である。例外的な天才は別として,数学に指導者は必要である。
数学は言語である。つまり,数式によるコミニケーションである。これが正しく使われないと,意志が伝わらないばかりか混乱を招く。ゼミではこの点も徹底していた。どういう表現が混乱を招くかも指導対象であり,必ずその場で修正し,言い直し書き直してきた。現場で長年に渡り由とし来た私流のやり方も,厳しく指導を受けた。
数学にとって,必要不可欠な者の1つとして『集中力』がある。時間と労力が伴うので,その集中力を持続させるには,忍耐力も必要である。そのためには,日常の自己管理,具体的には規則正しい生活を心掛けねばならない。例えば,睡眠不足,過労,二日酔いでは集中力を発揮できない。また,集中していると時間がたつのを忘れてしまい,結果として他のものを犠牲にすることになる。実際,1年間の私自身の研究をふりかえってもそうであった。仕事の合間を縫っての研究は大変で,結果として私的な趣味を犠牲にすることになった。
(4) 今後の進展
『数学とは一体なんなのか』というテーマは永遠である。 数学教育の立場からの私の持論を述べたい。数学は人類とともにあり,人類が長い年月をかけて築き上げてきたものである。しかもその中には,凡人からはるか掛け離れた天才たちが築き上げてきたものが多い。この歴史的側面からすれば,たとえ16世紀までとはいえ,その築き上げてきたものを小中高のわずか16年間で教育しようとすることに大きな矛盾を感じる。生徒は分からなくて当然でないかと思う。大量の数学嫌いがでる原因理由を掘り下げて行くと,ここに出るのではないかと思う。
数学とは時間と労力さえかければ,だれでもわかるようになる,できるようになるものである。しかし,このとき『わからない,できない』から『わかる,できる』ようになる構造が分かってないので,『わからない,できない』状態にどれくらいの時間と労力をかけたらよいのか先の見通しがつかない。見通しがつかないものには,人はだれしもなかなか時間と労力かけずらいものである。この点では指導する側の責任があるが,どんなにすばらしい指導がなされたとしても『わかる,できる』ようになるのには,あくまで本人の力によるしかない。
偉大な心理学者ピアジュは,直観的操作から具体的操作,具体的操作から形式的操作ができるようになる構造を児童心理学の立場で研究した。ただ,その内容は極めて難解で,その著作は相当の精読を要し,世界のどんな心理学者たちも理解するのは容易でないという。これを数学的に研究の対象にできないかというの私の夢である。
モデルはある。ルベーグ積分では,『連続関数は,階段関数の測度的収束』として定義されるが,階段関数とはあるところで急に不連続に値を変えてしまう関数で非線形である。また,自動制御理論ではリレー制御系(これも非線形)がある。
これが単なる夢物語でない理由がある。すでに,カオスの分野では『脳理論』『神経回路網理論』等,力学系としてのモデル化がはじまっている。
カオスを理解するには近代数学・現代数学の基礎的研究は済ましておかねばならない。今回,津田教授の『カオス』を受講して特にそう感じた。久保田教授の指導の下で『ルベーグ積分』は有界可測集合における有界可測関数まで終了した。有界という条件を取り除いた一般の可測集合における可測関数の残りを完結しながら,平行して近代数学・現代数学の基礎的研究も続けたい。
基礎研究と臨床研究の橋渡しをしながら,その研究成果を教育の現場に還元したい。また,現場にあっては,特に数学教師の間で臨床的研究にばかり偏らず,基礎的研究の必要性も指摘し,その先導役も果たしたい。具体的には,『数学教育における基礎研究』というテーマで研究したいと思う。
最後に,謝辞を申し上げたい。1年間の研究を継続できたのは,久保田教授,儀我教授,津田教授,そして大学院生の乾勝也氏をはじめ,北海道大学の関係者の方々のお陰であり感謝に絶えない。
また,職場の北海道石狩南高等学校では,研究室入室にあたり快く承諾していただいた渡部校長はじめ,ご理解支援していただいた職場の方々にもお礼を申し上げたい。
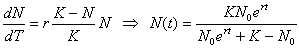 (N:固体数,t:時間,r,K:定数)
(N:固体数,t:時間,r,K:定数)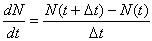 とおくと
とおくと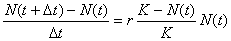
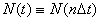 とおくと(B)は
とおくと(B)は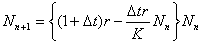
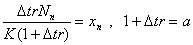 とおくと
とおくと