第2章　Mathematicaでグラフィックスを

第2章　Mathematicaでグラフィックスを

Mathematicaで２次元のグラフを作成するのには３つの方法があります。

Plot[関数式，｛変数，始めの値，終わりの値｝]
ParametricPlot[{x座標の指定，ｙ座標の指定｝，｛パラメ－タ－の指定｝]
Show[Graphics[ ]]

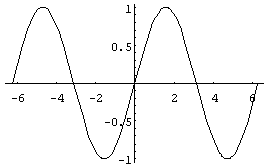例題１　y=sin Xのグラフを-2π≦X≦2πの範囲で作成せよ。


Plot[Sin[x],{x,-2Pi,2Pi}]

例題2　x=cos t，y=sin t（0≦t≦2π)のグラフを作成せよ。


ParametricPlot[{Cos[t],Sin[t]},{t,0,2Pi},

AspectRatio->Automatic,

Axes->False,

PlotStyle->{Thickness[0.0002]}]

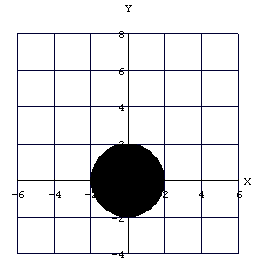例題3　原点中心、半径2の円盤を作成せよ。


Show[Graphics[Disk[{0,0},2]],

Axes->True,GridLines->Automatic,

AspectRatio->Automatic,

PlotRange->{{-6,6},{-4,8}},AxesLabel->{X,Y}]

北海道大学98年度

１．中心がそれぞれ、（－２、０）、（２、０）である半径１の円Ａ、Ｂを考える。円ＣがＡを含み、Ｂの外側にあり、しかも、Ａ，Ｂの両方に接しながら動くとき、次の問に答えよ。
（１）円Ｃの中心の軌跡を求めよ。
（２）円Ｃが直線ｙ＝２に接するとき、Ｃの半径を求めよ。

解答
（1）Cの中心をP，半径をｒ，Q(-2、0)、R(2、0)とする。
　AがCに内接し、BがCに外接するので、　　PQ＝ｒ-1、PR＝ｒ+1より
　　PR-PQ=2　従ってPの軌跡は双曲線になり
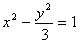　　　　ｘ＜0

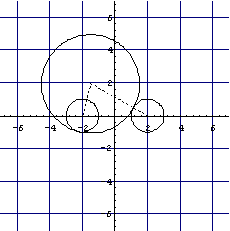これをMathematicaを利用して作図すると


Module[{A,B,cir},

 A={Circle[{-2,0},1]}; B={Circle[{2,0},1]};

 c[t_]:=Circle[{t,Sqrt[3 t^2-3]},1+Sqrt[4 t^2+4 t+1]];

 L[t_]:={Dashing[{0.01}],Line[{{2,0},

{t,Sqrt[3 t^2-3]},{-2,0}}]};

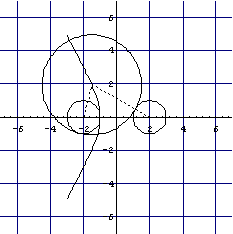
Show[Graphics[{A,B,c[-1.5],L[-1.5]},

Axes->True,PlotRange->{{-7,7},{-7,7}},

GridLines->Automatic,AspectRatio->Automatic]]]

Module[{文字,}]によって文字、数値、関数名を　指定するとModule内のみ設定され、それ以外　は無効となる。
Circle[{中心ｘ座標,中心ｙ座標},半径]
Line[{{x1,y1},{x2,y2}]：2点を結ぶ直線
Dashing[{線の長さ、スペ－スの長さ}]
Axes->True：ｘ軸、ｙ軸を入れる
GridLines->Automatic：方眼を入れる
PlotRange->｛｛ｘの範囲｝、｛ｙの範囲｝｝
関数の定義には、c[t_]:=変数の横にアンダ－バ－をつける

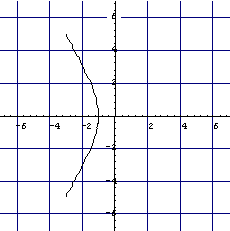双曲線を作図してみるプログラムは


Plot[{Sqrt[3 x^2-3],-Sqrt[3 x^2-3]},{x,-3,-1},

GridLines->Automatic,AspectRatio->Automatic,

PlotRange->{{-7,7},{-7,7}}]

Plot[{関数式1,関数式2},{変数,始めの値,終わりの値}
AspectRatio->縦横の比のオプション
　横の長さを1とした時の縦の長さでAspectRatioの値を設定する。Automaticとは縦横の比を等しくする

これらの2つのグラフを合成してみると


Show[%,%%]

％は1つ前のグラフィックを表す。
％％は2つ前のグラフィックを表す。

この2つのグラフィックを同時に重ねて表示する時はShow[　]を使う。

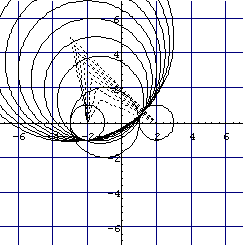これらの条件を満たす円を1つの座標軸上に重ねて表示してみるとどうなるのか考えてみましょう。


Module[{A,B,C,L},

 A={Circle[{-2,0},1]};

 B={Circle[{2,0},1]};

 c[t_]:=Circle[{t,Sqrt[3 t^2-3]},1+Sqrt[4 t^2+4 t+1]];

 L[t_]:={Dashing[{0.01}],Line[{{2,0},{t,Sqrt[3 t^2-3]},

{-2,0}}]};

C=Table[c[t],{t,-3,-1,0.25}];

L=Table[L[t],{t,-3,-1,0.25}];

Show[Graphics[{A,B,C,L},Axes->True,

PlotRange->{{-7,7},{-7,7}},

GridLines->Automatic,AspectRatio->Automatic]]]

さらにアニメ－ションを利用して動きのあるグラフィックを作成することも可能である。

（2）CがAを内部に含むので、Cがｙ＝2に接する時、Pはｙ＝2の下側に存在する。
P(x,y)とおくと、ｒ＝2-ｙ、PQ=ｒ-1より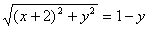　
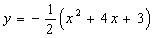を双曲線　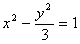へ代入しｘについて解くと
　ｘ＝-1、-7
　従って　ｙ＝0、-12　ｒ＝2、14
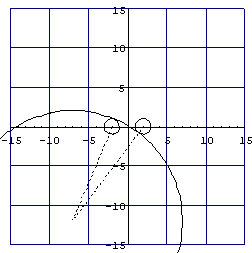
この解であるｘ＝-7、ｙ＝-12の時の作図をしてみよう。


Module[{A,B,cir},

 A={Circle[{-2,0},1]};

 B={Circle[{2,0},1]};

 c[t_]:=Circle[{t,-Sqrt[3 t^2-3]},

1+Sqrt[4 t^2+4 t+1]];

 L[t_]:={Dashing[{0.01}],Line[{{2,0},

{t,-Sqrt[3 t^2-3]},

{-2,0}}]};

Show[Graphics[{A,B,c[-7],L[-7]},Axes->True,

PlotRange->{{-15,15},{-15,15}}]]

【TOP】【BACK】【NEXT】