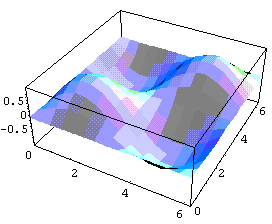
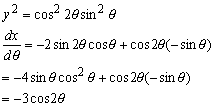Plot3D[Sin[x] Sin[y],{x,0,2Pi},{y,0,2Pi}]

俁師尦偺僌儔僼傪嶌惉偡傞偵偼俁偮偺曽朄偑偁傝傑偡丅
椺戣4丂z=sin x cos y (0亝x,y亝2兾)偺僌儔僼傪嶌惉偣傛丅
Plot3D[Sin[x] Sin[y],{x,0,2Pi},{y,0,2Pi}]

Plot3D[Sin[x] Sin[y],{x,0,2Pi},{y,0,2Pi},Mesh->False]
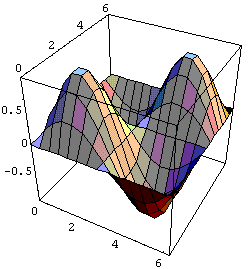
倶幉倷幉倸幉偺斾傪堦掕偵偡傞丂BoxRatios->{1,1,1}
Plot3D[Sin[x] Sin[y],{x,0,2Pi},{y,0,2Pi},BoxRatios->{1,1,1}]
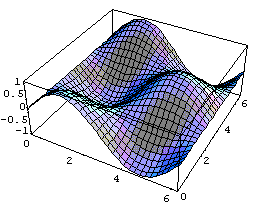
棫懱恾宍傪嵶偐偔偟偰昞尰偡傞丂PlotPoint->30丂僨僼僅儖僩抣15
椺戣5丂 z=sin X cos Y (0亝x,y亝2兾)偺僌儔僼傪棫懱恾宍傪嵶偐偔偟偰嶌惉偣傛
Plot3D[Sin[x] Cos[y],{x,0,2Pi},{y,0,2Pi},PlotPoints->30]
Parameter傪娷傫偩棫懱偺嶌惉丂ParametricPlot3D[{x(t),y(t),z(t)},{t,巒傔偺抣丆廔傢傝偺抣}]
椺戣6丂 x=cos t cos u丆 y=sin t cos u丆 z=sin u 丂(0亝t亝2兾丆 -兾/2亝t亝兾/2)偺僌儔僼傪嶌惉偣傛丅
ParametricPlot3D[{Cos[t] Cos[u],Sin[t] Cos[u],Sin[u]},
{t,0,Pi},{u,-Pi/2,Pi/2},Boxed->False]
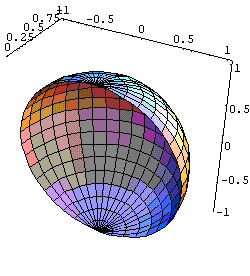
夞揮懱偺嶌恾丂<<Graphics'SurfaceOfRevolution'偺僷僢働亅僕傪嵟弶偵儘亅僪偡傞丅
丂 丂Mathematica偺嵟傕摼堄偲偡傞僌儔僼傿僢僋婡擻傪棙梡偟偨僞僀儉儕亅側栤戣偑偁偭偨偺偱徯夘偟傑偡丅
杒奀摴戝妛98擭搙
俀丏娭悢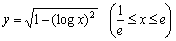 偺僌儔僼傪俠偲偡傞丅
偺僌儔僼傪俠偲偡傞丅
丂師偺栤偵摎偊傛丅偨偩偟丆懳悢偼帺慠懳悢偲偟丆倕偼偦偺掙偲偡傞丅
乮侾乯 俠忋偺揰俙偵偍偗傞俠偺愙慄偑尨揰俷乮侽丆侽乯傪捠傞傕偺偲偡傞丅偙偺偲偒丆揰俙偺倶嵗昗傪媮傔傛
乮俀乯 俠偲倶幉偱埻傑傟偨恾宍傪丄倶幉偺傑傢傝偵侾夞揮偟偰摼傜傟傞棫懱偺懱愊傪媮傔傛丅
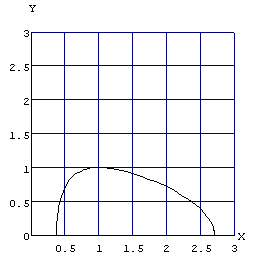 夝摎
夝摎
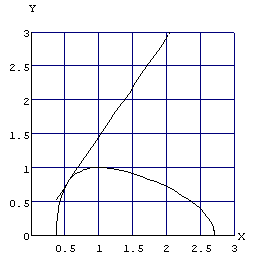
巒傔偵偳傫側僌儔僼偵側傞偺偐嶌惉偡傞偲
Plot[Sqrt[1-Log[x]^2],{x,1/E,E},
GridLines->Automatic,AspectRatio->1,
AxesLabel->{X,Y},PlotRange->{{0,3},{0,3}}]
丂
 傪旝暘偟偰倶亖倲偵偍偗傞愙慄偺曽掱幃傪媮傔傞偲丄
傪旝暘偟偰倶亖倲偵偍偗傞愙慄偺曽掱幃傪媮傔傞偲丄
 乧嘆
乧嘆
偙偺媮傔偨愙慄傪丂0.5亙倲亙1偺斖埻偱偄傠偄傠嶌恾偟偰傒傛偆丅
Plot[Evaluate[Table[-Log[t]/{t Sqrt[1-Log[t]^2]}
{x-t}+Sqrt[1-Log[t]^2],
{t,0.5,1,0.05}]],{x,0,E},GridLines->Automatic,
AspectRatio->1,AxesLabel->{X,Y},
PlotRange->{{0,3},{0,3}}]
Show[%,%%]
 偄傠偄傠側愙慄傪摨帪偵昞帵偡傞偵偼愙慄偺儕僗僩傪嶌惉偡傞丅
偄傠偄傠側愙慄傪摨帪偵昞帵偡傞偵偼愙慄偺儕僗僩傪嶌惉偡傞丅
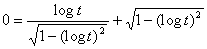
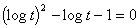 傛傝
傛傝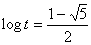
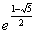 偲側傞丅
偲側傞丅
 丂崱搙偼丄Mathematica偺旝暘寁嶼婡擻傪棙梡偟偰愙慄傪昞尰偟偰傒傛偆丅
丂崱搙偼丄Mathematica偺旝暘寁嶼婡擻傪棙梡偟偰愙慄傪昞尰偟偰傒傛偆丅
Mathematica傪棙梡偟偰摫娭悢傪媮傔傞1偮曽朄偼丄f[x]傪掕媊偟偰偍偒丄f'[x]偲擖椡偟偰摫娭悢傪摼傞曽朄傪梡偄傞丅
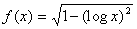 偲偍偄偰摫娭悢傪媮傔傞偲
偲偍偄偰摫娭悢傪媮傔傞偲
f[x_]:=Sqrt[1-Log[x]^2];
f'[x]
Log[x]
丂丂-(-------------------)
x Sqrt[ 1 - Log[x] 2 ]
 偺偍偗傞愙慄傪嶌恾偟偨丅
偺偍偗傞愙慄傪嶌恾偟偨丅
f[x_]:=Sqrt[1-Log[x]^2];
p=E^((1-Sqrt[5])/2);
g[x_]:=f'[p] (x-p)+f[p];
Plot[{f[x],g[x]},{x,1/E,E},
GridLines->Automatic,AspectRatio->1,
AxesLabel->{X,Y},PlotRange->{{0,3},{0,3}}]
乮2乯偼夞揮懱偺栤戣偱偁傞丅Mathematica 偺3D僌儔僼傿僢僋僗婡擻傪棙梡偡傞丅
倶幉傪拞怱偲偟偰夞揮偟偨嬋柺偺嶌惉偱偁傞偺偱丄僷僢働亅僕Graphics偺拞偺SurfaceOfRevolution偲偄偆僷僢働亅僕傪儘亅僪偡傞丅
<<Graphics`SurfaceOfRevolution`
SurfaceOfRevolution[Sqrt[1-Log[x]^2],{x,1/E,E},
{t,Pi,2 Pi},RevolutionAxis->{1,0,0},
ViewPoint->{-1.334,-2.381,2.000}]
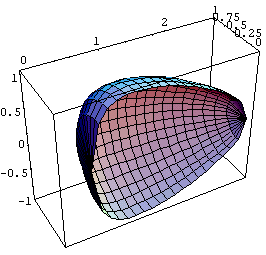 塃偺棫懱恾偺懱愊傪媮傔傞偲丄
塃偺棫懱恾偺懱愊傪媮傔傞偲丄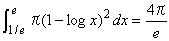 偲側傞丅
偲側傞丅
Integrate[Pi (1-Log[x]^2),{x,1/E,E}]
4 Pi
----
E
嫗搒戝妛1998擭搙屻婜
3.帺慠悢値偵懳偟偰丄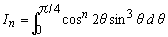 偲偡傞丅
偲偡傞丅
乮1乯I2偺抣傪媮傔傛丅
乮2乯倶倷暯柺忋偱尨揰偐傜P(x,y)傊偺嫍棧傪倰丄倶幉偺惓偺曽岦偲敿捈慄OP偺側偡屖搙朄偵傛傞妏傪兤偲偡傞丅曽掱幃r=sin2兤乮0亝兤亝兾/2乯偱昞偝傟傞嬋慄傪丄捈慄倷亖倶偺廃傝偵夞揮偟偰摼傜傟傞嬋柺偑埻傓棫懱偺懱愊傪V偲偡傞偲偒丄V=3兾I3+2兾I2偲昞偣傞偙偲傪帵偣丅
夝摎
乮1乯偼抲姺愊暘傪巊偭偰
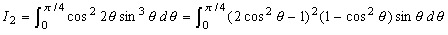
t=cos兤偲偍偔dt=-sin兤倓兤
丂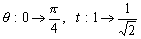 偲愊暘斖埻偑曄傢偭偰
偲愊暘斖埻偑曄傢偭偰
丂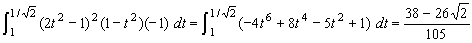
偲寁嶼偱偒傞丅
Mathematica偺掕愊暘寁嶼婡擻Integrate[f[x],{x,a,b}]傪棙梡偟偰傒傞偲丄
Integrate[Cos[2 x]^2 Sin[x]^3,{x,0,Pi/4}]
38 26 Sqrt[2]
--- - -------------
105 105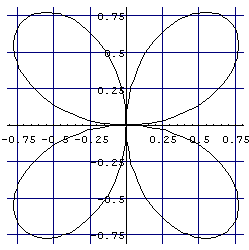 乮2乯偼嬌嵗昗偱昞帵偝傟偰偄傞偺偱丄僷僢働亅僕"Graphics`Graphics`"傪儘亅僪偡傞丅
乮2乯偼嬌嵗昗偱昞帵偝傟偰偄傞偺偱丄僷僢働亅僕"Graphics`Graphics`"傪儘亅僪偡傞丅
Needs["Graphics`Graphics`"]
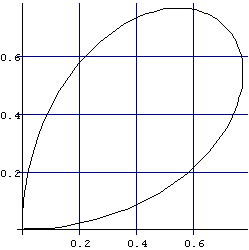
PolarPlot[Sin[2 t],{t,0,2 Pi},
GridLines->Automatic,AspectRatio->Automatic]
崱搙偼丄僷儔儊亅僞亅倲傪梡偄偰僌儔僼傪嶌惉偟偰傒傞丅
僷儔儊亅僞亅倲偺斖埻偼丄0亝t亝兾/2偲偡傞丅
ParametricPlot[{2 Sin[t] Cos[t]^2,2 Sin[t]^2 Cos[t]},
{t,0,Pi/2},GridLines->Automatic,AspectRatio->Automatic]
 塃恾傪丄捈慄倷亖倶傪夞揮幉偲偟偰夞揮偟偨棫懱傪嶌惉偡傞丅擟堄偺幉偵娭偡傞夞揮偼丄RevolutionAxis->{倶惉暘丄倷惉暘丄倸惉暘}偲偟偰昞帵偡傞偙偲偑偱偒傞丅
塃恾傪丄捈慄倷亖倶傪夞揮幉偲偟偰夞揮偟偨棫懱傪嶌惉偡傞丅擟堄偺幉偵娭偡傞夞揮偼丄RevolutionAxis->{倶惉暘丄倷惉暘丄倸惉暘}偲偟偰昞帵偡傞偙偲偑偱偒傞丅
<<Graphics`SurfaceOfRevolution`
SurfaceOfRevolution[{2 Sin[t] Cos[t]^2,
2 Sin[t]^2 Cos[t]},
{t,0,Pi/4},{p,0,Pi},RevolutionAxis->{1,0,1}]
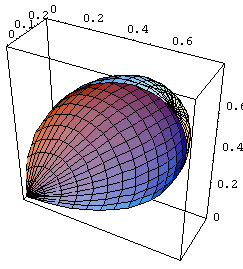 慡懱傪45搙夞揮偟偰丄嬋慄偼
慡懱傪45搙夞揮偟偰丄嬋慄偼
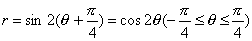
偙傟偼x=cos2兤 soc兤丆y=cos2兤 sin兤偲側傝