 搶嫗戝妛1996擭
搶嫗戝妛1996擭
戞3復丂Mathematica偱傾僯儊亅僔儑儞
丂 傾僯儊亅僔儑儞傪嶌惉偡傞偵偼丄<<Graphics乫Animation乫偺僷僢働亅僕傪嵟弶偵儘亅僪偡傞丅
傾僯儊亅僔儑儞幚墘
傾僯儊亅僔儑儞傪棙梡偡傞偲棟夝偟傗偡偄擖帋栤戣傪庢傝忋偘偰傒傛偆
 搶嫗戝妛1996擭
搶嫗戝妛1996擭
倶倷倸亅嬻娫撪偺墌拰x2+y2=R2乮R>0乯傪懁柺偲偡傞梕婍偵丄悈偑z=0偲堦抳偡傞傛偆偵倸亝0偺晹暘偵悈偑擖偭偰偄傞丅倸亞0偵懳偟偰掕媊偝傟偨楢懕側娭悢r(z)偱丄r(0)=0丄0亝r(z)亝R傪枮偨偡傕偺偲偡傞丅xz暯柺撪偺晄摍幃0亝x亝r(z)丆倸亞0偱昞偝傟傞椞堟傪丄倸幉偺廃傝偵侾夞揮偟偰偱偒傞夞揮懱傪枅昩侾偺懍偝偱壓偵摦偐偡偲丄倲昩屻偵偼悈柺偑z=f(t)偵忋徃偡傞偲偄偆丅T亞0偵懳偟偰丄f(t)=et亅t亅1偱偁傞帪丄娭悢r(z)傪寛掕偣傛丅
夝摎
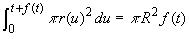 椉曈傪倲偱旝暘偡傞偲
椉曈傪倲偱旝暘偡傞偲
兾r(t+f(t))2(1+f'(t))=兾R2f'(t)
偙傟偵f(t)=et亅t亅1傪戙擖偡傞丅摿偵f'(t)=et亅1傕戙擖偡傞偲丄
r(et亅1)et=R2(et亅1)
et亅1亖z偲偍偔偲丄r(z)2(z+1)=R2z傛傝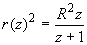
t亞0傛傝倸亞0丂丂亪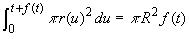 乧乮摎乯
乧乮摎乯
悈柺偺忋徃傪傾僯儊亅僔儑儞偱昞尰偟偰傒傞偲
g[x_,k_]:=x^2/(4-x^2)-k
f[k_]:=E^k-k-1
Do[Plot[{g[x,k],0,
f[k]},{x,-1.95,1.95},PlotRange->{{-2,2},{-4,15}},
PlotStyle->{Thickness[0.01]},
GridLines->Automatic,
AspectRatio->1.5],{k,0,3,0.5}]
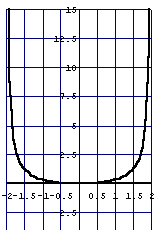
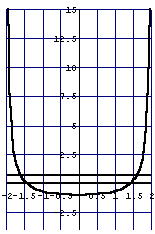
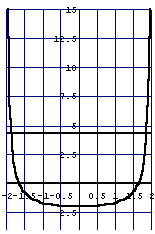
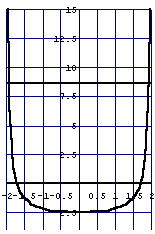
峏偵丄傾僯儊亅僔儑儞壔偡傞偲棟夝偟傗偡偄栤戣傪峫偊偰傒傛偆丅
杒奀摴戝妛屻婜丂4
悈暯側婘偺忋偺抲偐傟偨丄侾曈偺挿偝1偺棫曽懱偺僈儔僗梕婍偵丄偦偺梕愊偺1/4偺検偺僀儞僋偑枾晻偝傟偰偄傞丅恾1偵帵偡傛偆偵丄梕婍偺撪晹偵懁柺俷俙俛俠偐傜嫍棧倎丄侽亙倎亙侾偺埵抲偵丄巺偑曈俷俠偵暯峴偵挘傜傟偰偄傞丅掙曈俷俙傪婘偺忋偵屌掕偟丄偦傟傪夞揮幉偲偟偰丄恾2偺傛偆偵丄梕婍傪惷偐偵90亱夞揮偝偣偰巭傔偨丅偙偺夁掱偵偍偄偰丄彮側偔偰傕堦搙僀儞僋偵怗傟偨巺偺晹暘偺挿偝傪丄f(a)偲偡傞丅師偺栤偄偵摎偊傛丅
偨偩偟丄僈儔僗偺岤偝偼柍帇偣傛丅
丂乮1乯f(1/2)=1/4傪帵偣丅
丂乮2乯1/4亙倎亙1/2偺偲偒丄f(倎)=1/8倎傪帵偣丅
夝摎
乮1乯倎=1/2偺帪丄恾2丄3丄4斣栚偵偍偄偰丄僀儞僋偺崅偝偼OA=1丄梕愊1/4傛傝丄柺愊1/4偱堦掕丅
| 乮鶣乯1/4亙倶亙1/2偺帪 | 乮鶤乯1/2亝倶亙1偺帪 | 乮鶥乯倶亖1偺帪 |
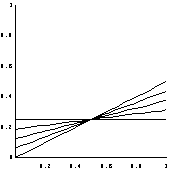 |
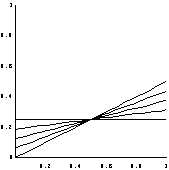 |
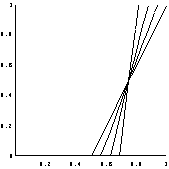 |
柺愊丗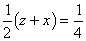 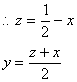 傛傝丄y=1/4 |
柺愊丗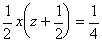 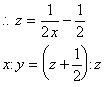 傛傝丄倷=倶(1亅倶) |
偙傟埲崀丄巺偼僀儞僋偼巺偵怗傟側偄偺偱丄 亪倷=0 |
埲忋傛傝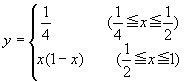 偲側傞丅傛偭偰丄嵟戝抣偼1/4f(1/2)=1/4
偲側傞丅傛偭偰丄嵟戝抣偼1/4f(1/2)=1/4
偙偺條側壖憐幚尡揑栤戣偼傾僯儊亅僔儑儞壔偟偰傒傞偲丄棟夝偟傗偡偄丅
Box={{0,0},{0,1},{-1,1},{-1,0},{0,0}};
Ito={{-1/2,0},{-1/2,1}};
Ro[t_]:={{Cos[t],-Sin[t]},{Sin[t],Cos[t]}};
Lev[t_]:=Which[N[Tan[t]]<0.5,{{-1,1/4-Tan[t]/2},{0,1/4+Tan[t]/2}},
0.5<=N[Tan[t]]<=1.5,{{-2/(1+2 Tan[t]),0},{0,1/4+Tan[t]/2}},
1.5<N[Tan[t]],{{-1/4-1/(2 Tan[t]),0},{-1/4+1/(2 Tan[t]),1}}]
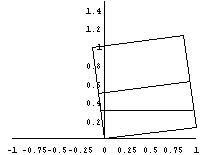
Do[Show[Graphics[{Line[Box.Ro[t]],Line[Ito.Ro[t]],
Line[Lev[t].Ro[t]]}],
AspectRatio->Automatic,
Axes->True,PlotRange->{{-1,1},{0,1.5}}],{t,0,N[Pi/2]-0.001,N[Pi/24]}]
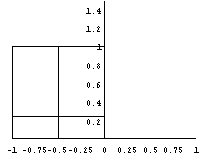 | 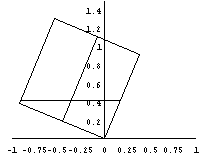 | 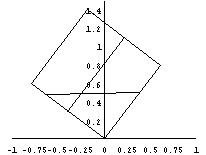 |
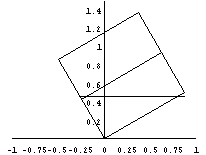 |  | 丂 |