 |  |  |
 |  |
第4章 Mathematicaでフラクタル数学
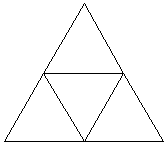
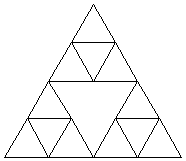
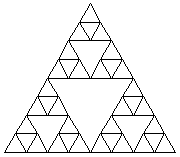
1975年IBMワトソン研究所のマンデルブロ−が発見した図形で、「フラクタル」という言葉をこの世に送り出しました。リアス式海岸、山・川の起伏、生物現象の中にどんどん発見されてている自己相似構造を持った図形を「フラクタル図形」と呼ぶのですが、コンピュ−タ・グラフィックの発展により比較的に簡単に作図出来るようになりました。今回は「シェルピンスキ−の三角形」「コッホ曲線の3次元化された図形」「植物の成長」について「mathematica」を使って作成してみました。問題1 シェルピンスキ−の三角形
フラクタル数学の代表的な問題で、第1回目として正三角形の3辺を2等分して中点どうしを結び、中心部の逆三角形を除く3個の縮小された正三角形を作成する。第2回目として、この3個の縮小された正三角形において、更に3辺を2等分して中点どうしを結び、中心部の逆三角形を除く3個の縮小された正三角形を作成する。以下同様の繰り返しを行うと、次々と自己相似形の三角形が完成していきます。
Clear[spawn]
spawn[{a_,b_,c_,a_}]:=
Block[{ab=(a+b)/2,bc=(b+c)/2,ac=(a+c)/2},
{{a,ab,ac,a},{b,bc,ab,b},{c,ac,bc,c}}];
spawn[l_List]:=
Flatten[Map[spawn,l],1]/;Length[l[[1]]]>1;
Do[Show[Graphics[{Thickness[0.001],Line /@
Nest[spawn,{{0,0},
{1/2,Sqrt[3]/2},{1,0},{0,0}},k]}],
AspectRatio->Sqrt[3]/2],{k,1,7}]
 |  |  |
 |  |
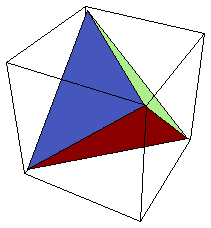
問題2 コッホ曲線の3次元化された図形
正4面体上の4つの正三角形の上に、元の正三角形の1辺の長さの半分の正4面体を作成し続けると、究極的には、どんな図形になるか?これは、1997年1月「北海道高等学校数学コンテスト」に出題した問題であります。
A1={1,0,0};A2={0,1,0};A3={0,0,1};
norm[v_]:=Sqrt[v.v]
Gaiseki[v_,w_]:={Det[{A1,v,w}],Det[{A2,v,w}],Det[{A3,v,w}]}
new[{x_,y_,z_}]:=norm[y-x] Gaiseki[y-x,z-x]/
(norm[Gaiseki[y-x,z-x]] Sqrt[6])+(x+y+z)/3
data[{x_,y_,z_}]:={{x,(x+y)/2,(x+z)/2},
{(x+y)/2,y,(z+y)/2},{(x+z)/2,(z+y)/2,z},
{(x+z)/2,(x+y)/2,new[{x,y,z}]},{(x+y)/2,(z+y)/2,new[{x,y,z}]},
{(z+y)/2,(x+z)/2,new[{x,y,z}]}}
fractalize[{x_,y_,z_}]:=Map[Polygon[#]&,data[{x,y,z}]]
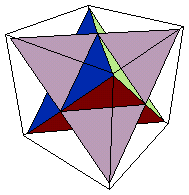
DD[0]={{{1,1,-1},{-1,1,1},{1,-1,1}},
{{-1,-1,-1},{1,1,-1},{1,-1,1}},
{{-1,-1,-1},{1,-1,1},{-1,1,1}},
{{-1,-1,-1},{-1,1,1},{1,1,-1}}};
T0=Show[Graphics3D[Map[Polygon[#]&,DD[0]]]]
Do[Snoopy[n_]:=Part[DD[0],n],{n,1,Length[DD[0]]}];
T1=Show[Graphics3D[Table[fractalize[v]/.{v->Snoopy[i]},
{i,1,Length[DD[0]]}],
ViewPoint->{1.7,1.3,1.3}]]

DD[1]=Flatten[Table[data[v]/.{v->Snoopy[i]},
{i,1,Length[DD[0]]}],1];
Do[Mic[n_]:=Part[DD[1],n],{n,1,Length[DD[1]]}];
T2=Show[T1,Graphics3D[Table[fractalize[v]/.
{v->Mic[i]},{i,1,Length[DD[1]]}],
ViewPoint->{2,1.3,1.3}]]

DD[2]=Flatten[Table[data[v]/.{v->Mic[i]},
{i,1,Length[DD[1]]}],1];
Do[Donald[n_]:=Part[DD[2],n],{n,1,Length[DD[2]]}];
T3=Show[T1,Graphics3D[Table[fractalize[v]/.{v->Donald[i]},
{i,1,Length[DD[2]]}],ViewPoint->{2,1.3,1.3}]]
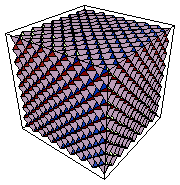
DD[3]=Flatten[Table[data[v]/.{v->Donald[i]},
{i,1,Length[DD[2]]}],1];
Do[Poo[n_]:=Part[DD[3],n],{n,1,Length[DD[3]]}];
T4=Show[T1,Graphics3D[Table[fractalize[v]/.{v->Poo[i]},
{i,1,Length[DD[3]]}],ViewPoint->{2,1.3,1.3}]]
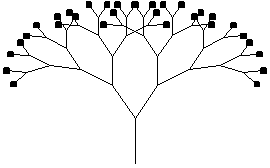
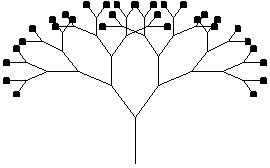
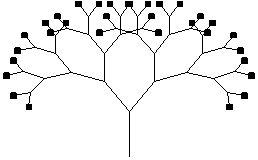
問題3 植物の成長
Washington大学のEric Halsay の作成した、「Tree」というプログラムを見てみよう。自然界に存在する、植物の成長をコンピュ−タ・グラフィックでシュミレ−ションしてみたもので非常に面白い。
depth:枝分かれの深さ、何回枝分かれをするのか。
length:1番下の枝の長さ。
angle:2つの枝分かれするときの、開き具合。
ratio:枝が次のレベルに進むときの縮小する割合。
以上4つの変数で「Tree」の関数を作成してある。
Clear[initialize]
initialize[start_List:{0.,0.},dim_Integer:1000]:=
(path=Table[Null,{dim}];
X=start//N;U={1.,0.};path[[1]]=X;count=1)
right[a_]:=
U={{t1=Cos[aa=a Degree//N],t2=Sin[aa]},{-t2,t1}}.U
left[a_]:=right[-a]
forward[s_]:=path[[++count]]=(X+=s U)
back[s_]:=forward[-s]
finished:=path=Take[path,count]
showturtlepath:=(finished;
Show[Graphics[Line[path]],PlotRange->All,
AspectRatio->1];)
Attributes[Tree]=Listable
Listable
branch[depth_Integer,length_,angle_,ratio_]:=(
forward[length];left[angle/2];
If[depth>0,branch[depth-1,length ratio,angle,ratio],
AppendTo[points,X]];right[angle];
If[depth>0,branch[depth-1,length ratio,angle,ratio]];
left[angle/2];back[length];)
Tree[depth_Integer,length_,angle_,ratio_]:=(initialize[];
points={ };left[90];
If[depth>0,branch[depth,length,angle,ratio]];finished;
Show[Graphics[{Line[path],PointSize[0.02],Point/@points}],
PlotRange->All])
Tree[5,1,Range[45,90,2.5],0.8]
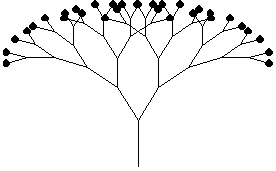 | 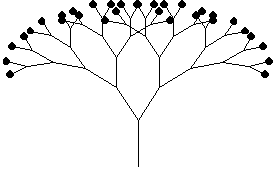 |
 |  |
 |