 Mathematicaでプログラムすると複素関数f(z)=z2によって複素平面上の点が、どのような、もう一つの複素平面に写るのかを調べる問題である。
Mathematicaでプログラムすると複素関数f(z)=z2によって複素平面上の点が、どのような、もう一つの複素平面に写るのかを調べる問題である。
第5章 Mathematicaで複素数
複素関数の問題を考えてみよう。特に(1)の問題が複素数関数の初等関数に関する基礎的な問題で興味深い。北海道大学98年度
4.複素数平面において、複素数 1,1+2i,2i,z,ωを表す点を、それぞれA,B,C,P,Qとする。この時、次の問いに答えよ。
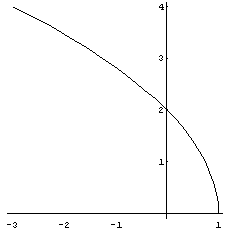
(1)点Pが線分AB上をAからBまで動くとき、複素数z2を表す点は、複素数平面上で、どのような図形をえがくか、式で表し図示せよ。
(2)△AQCが点Qを直角の頂点とする直角二等辺三角形になるとき、複素数ωを求めよ。
解答(1)
点Pが点AからBまで線分ABを動くとき、z=1+ti (0≦t≦2)とおくとz2=1-t2+2ti
z=x+yi(x,yは実数)と置くとx-1-t2,y=2tとパラメ−タ−表示できてtを消去すると、
x=1-y2/4(1≦t≦2)より、0≦y≦4となる。
 Mathematicaでプログラムすると複素関数f(z)=z2によって複素平面上の点が、どのような、もう一つの複素平面に写るのかを調べる問題である。
Mathematicaでプログラムすると複素関数f(z)=z2によって複素平面上の点が、どのような、もう一つの複素平面に写るのかを調べる問題である。
Module[{sy,sy2},
sy=Table[1+y I,{y,0,2,0.1}];
sy2=Map[{Re[#^2],Im[#^2]}&,sy];
Show[Graphics[{Table[Line[sy2],
{y,-3,3,0.5}]}],
Axes->True,AspectRatio->1]]
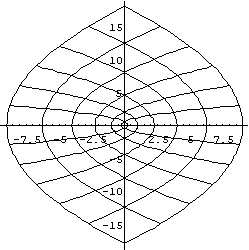 上の問題を一般的に拡張しみると複素関数f(z)=z2の性質が良く理解できる。
上の問題を一般的に拡張しみると複素関数f(z)=z2の性質が良く理解できる。
Module[{sx,sx2,sy,sy2},
sx=Table[x+y I,{x,-3,3,0.1}];
sy=Table[x+y I,{y,-3,3,0.1}];
sx2=Map[{Re[#^2],Im[#^2]}&,sx];
sy2=Map[{Re[#^2],Im[#^2]}&,sy];
Show[Graphics[{Table[Line[sx2],{y,-3,3,0.5}],
Table[Line[sy2],{x,-3,3,0.5}]}],
Axes->True,AspectRatio->1]]
北海道大学1998年度
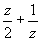 が0以上2以下の実数であるような複素数z(z≠0)を表す複素平面上の点の集合を、式で表し、図示せよ。
が0以上2以下の実数であるような複素数z(z≠0)を表す複素平面上の点の集合を、式で表し、図示せよ。
解答
単にこの問題を解法するよりも、複素関数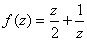 とは、どんな複素関数を表しているのだろうか?という事にに興味がもたれる。Mathematicaを使えば、複素数関数を幾何学的に経験することができる。今回は、「ExploringMathematicswithMathematica」(T・WグレイJ・グリン著)トッパンより「第19章複素写像あるいは錯綜したもの」より「ComplexMapPlot」というパッケ−ジをロ−ドして複素関数の幾何学的変化を見てみよう。
とは、どんな複素関数を表しているのだろうか?という事にに興味がもたれる。Mathematicaを使えば、複素数関数を幾何学的に経験することができる。今回は、「ExploringMathematicswithMathematica」(T・WグレイJ・グリン著)トッパンより「第19章複素写像あるいは錯綜したもの」より「ComplexMapPlot」というパッケ−ジをロ−ドして複素関数の幾何学的変化を見てみよう。
ComplexMapPlot[z/2+1/z,z,
RectangularGrid[{{-1,1},{-1,1}}]]
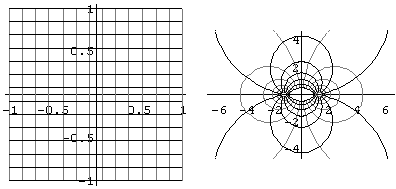 ComplexMapPlot で関数を定義して、RectangularGridで直交座標での変換を見ることができる。
ComplexMapPlot で関数を定義して、RectangularGridで直交座標での変換を見ることができる。
ComplexMapPlot[z/2+1/z,z,
PolarGrid[{0,0},{0.1,5}]]
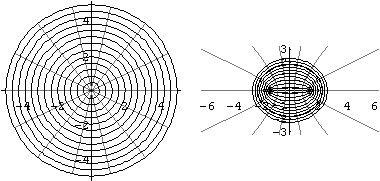 PolarGrid では、極座標での変換をみることができる。
PolarGrid では、極座標での変換をみることができる。いずれにしても、複素関数に関する問題も多く出題されておりこれらの、幾何学的な変化を見ることができるのは、とても楽しみな事である。
複素関数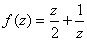 において、実軸上に中心があり、円周が点(-1,0)を通過する円の中心を実軸に沿って移動していくと、複素関数
において、実軸上に中心があり、円周が点(-1,0)を通過する円の中心を実軸に沿って移動していくと、複素関数 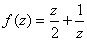 で変換された図形はどんな形になるのであろうか?
で変換された図形はどんな形になるのであろうか?
Do[ComplexMapPlot[z/2+1/z,z,{Circle[{0.3,n},0.3+1]},
PlotRange->{{-2,3.5},{-2,2}}],{n,-0.3,0.3,0.05}]
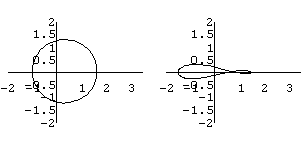 右図の様に、飛行機の翼のような形に変換される。
右図の様に、飛行機の翼のような形に変換される。
更に、円の中心のX成分と半径を固定して虚軸に沿って円を移動していくと、複素関数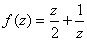 で変換された図形はどんな形になるのであろうか?
で変換された図形はどんな形になるのであろうか?