次のシミュレーションをみてください。同じ振幅をとっても、円周上を回る速さの違いによって違う波を描くことになります。
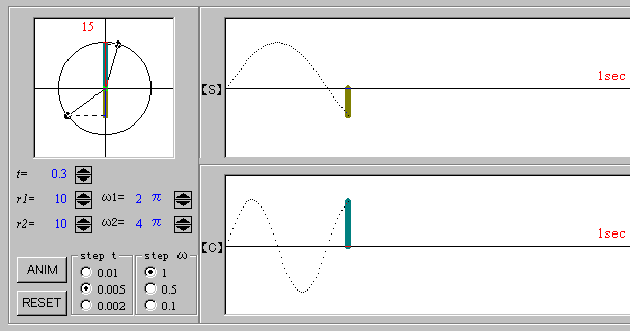
円周上を回る速さが速ければ速いほど、より多くの波を描くことになります。このように、時間によって上下する波の場合、
 1_2 周期・周波数・角速度
1_2 周期・周波数・角速度
次のシミュレーションをみてください。同じ振幅をとっても、円周上を回る速さの違いによって違う波を描くことになります。

円周上を回る速さが速ければ速いほど、より多くの波を描くことになります。このように、時間によって上下する波の場合、
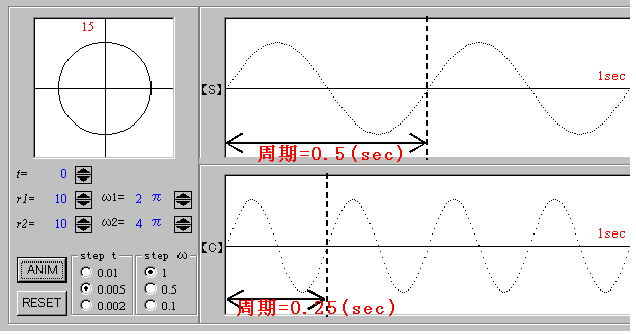
さてここで、角θも時間とともに変化するので、θもtの式で表すことができるはずです。そこで、角の増える速度を考えてみましょう。
1秒間に進む角度のことを「角速度」といい、ω(オメガ)で表します。すなわち、式でいうと
| 角速度(ω)=角度(θ)/時間(t) |
これまででてきた周期、周波数、角速度の3つの関係をまとめると、次のようになります。
(sec) |
(Hz) | (°/sec) | ||
| ア | 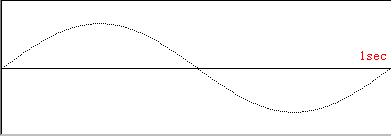 | (2π) | ||
| イ | 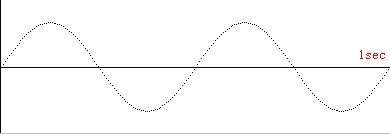 | (4π) | ||
| ウ | 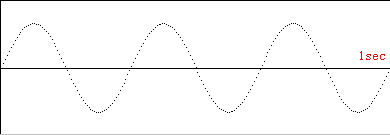 | (6π) | ||
| エ | 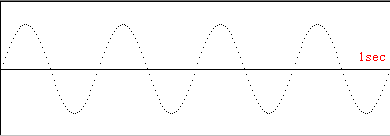 | (8π) | ||
| オ |  | (π) | ||
| カ |  | (2/5π) |
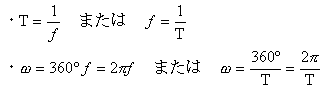
という関係が成り立ちます。また、ω=θ/t より θ=tωとなり、sin波,cos波を時間tの関数と考えると、次の式が成り立ちます。

|
シミュレーションプログラムのダウンロード ◎実行プログラム「sc_wave_2.exe」(約40KB) ◎カスタムコントロール「Spin32.ocx」(約52KB) ⇒「Spin32.ocx」はWindows\Systemフォルダに置いてください |