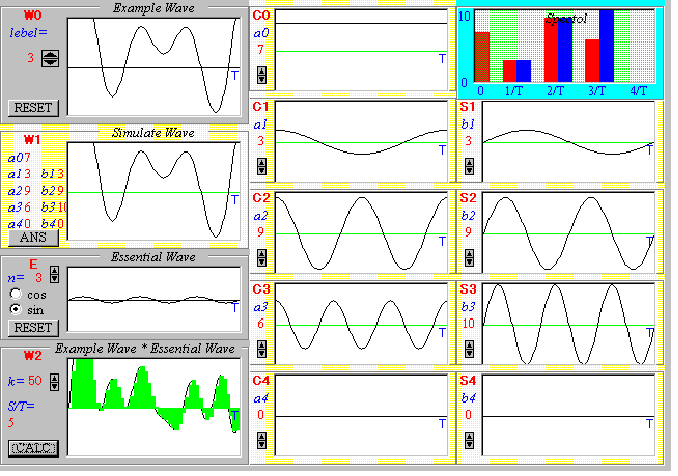
次のシミュレーションプログラムをみてください。いっぱいグラフが並んでいますね。左上の【W0】が分解したい問題の波です。そして、その下の【W1】が自分で合成していく波です。【W1】は右に並んでいる9つの波を合成して作ります。定数波【C0】とｓｉｎ波【C1】〜【C4】、ｓｉｎ波【S1】〜【S4】を組み合わせて、最終的に問題の波【W0】を作り上げてみましょう。それぞれの波のスピンボタンを操作すれば、振幅が変わります。なお、それぞれの波は全て1周期分Tでそろえてあります。

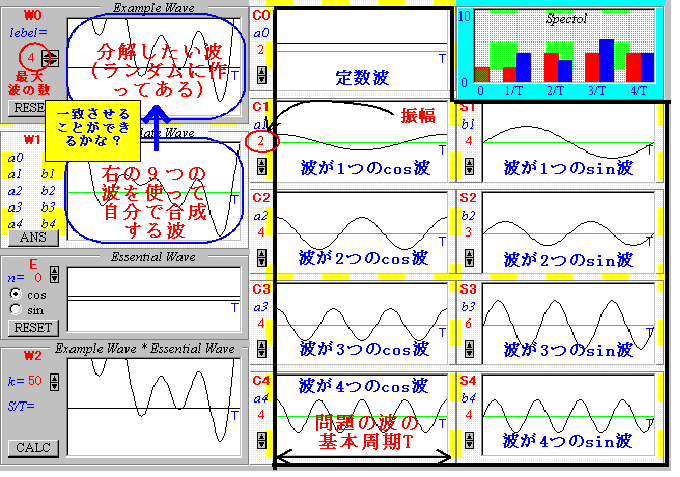
　さっそく始めていきましょう。先ほどまで調べてきたａ₀からａ_n，ｂ_nの求め方をもとに、順に係数を決定していきましょう。

　波【W0】のところにあるlebelボタンによって、合成されている波の最大数を決定できるようになっています。とりあえずlebel=1、すなわち定数波【C0】と基本周期の中に波が1個のｓｉｎ波【C1】、ｃｏｓ波【S1】の3つの波から合成されている波を分解してみましょう。次のグラフが分解したい問題の波とします。

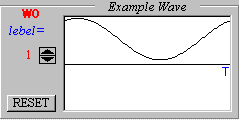
(1)　ａ₀を決定する

　まずは係数ａ₀を決定していきましょう。先ほどわかったように、ａ₀は「複雑な波ｆ(ｔ)の1周期分の面積を求めて、周期Tで割る」ことによって求まりました。式でいうと、

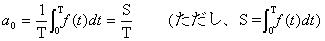
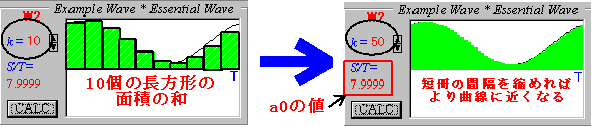
　さて、ここで波ｆ(ｔ)の1周期分の面積はどうやって求めればよいのでしょう。ここで登場するのが「積分」の考え方です。縦に短冊に切り取り、できた長方形の面積を合計すると、だいたいの面積がでてきますね。こうして求めた面積を基本周期Tで割ると、係数ａ₀が求まります。

(2)　ａ_nを決定する

　次に係数ａ_nを決定していきましょう。ａ_nを求めるのは少し複雑で、「複雑な波ｆ(ｔ)に同じ周波数の波をかけ、その1周期分の面積を周期Ｔで割り2倍する」ことによって求まりました。式でいうと、

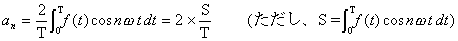
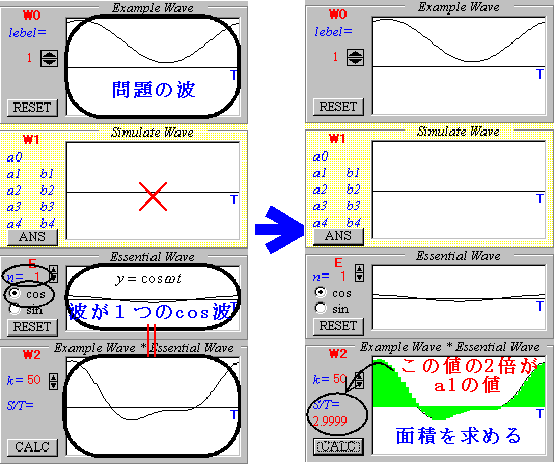
　それではａ₁を求めましょう。1周期Ｔの間に波が1つのｃｏｓ波　ｙ＝ｃｏｓωｔ　をかけ合わせます。そして、先ほどと同様にしてその間の面積を出し、Ｔで割ってみましょう。波【W2】のところにでてくるＳ/Ｔの数値がその値になります。その値の2倍が求めるａ₁の値です。

(3)　ｂ_nを決定する

　同様にして係数ｂ_nを決定しましょう。ｂ_nを求める式は、

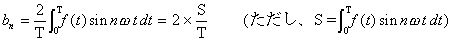
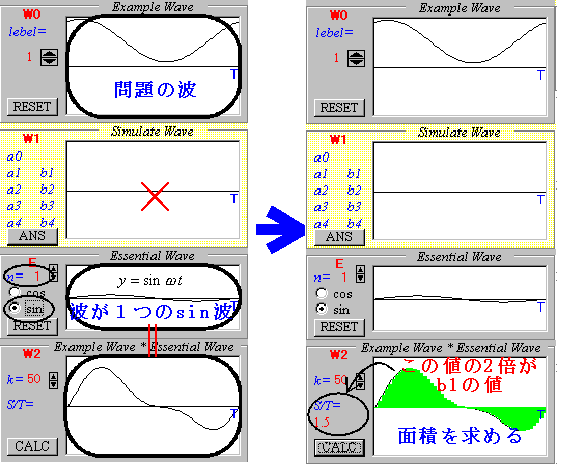
　ｂ₁を求めるために、1周期Ｔの間に波が1つのｓｉｎ波　ｙ＝ｓｉｎωｔ　をかけ合わせます。そして、先ほどと同様にしてその間の面積を出し、Ｔで割ってみましょう。その値の2倍が求めるｂ₁の値です。

　(1)〜(3)をまとめると、ａ₀＝8，ａ₁＝6，ｂ₁＝3　となります。式でいうと、

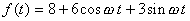
　遂に波の分解ができました！

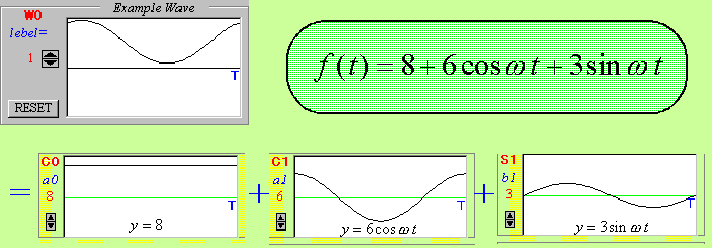
　分解した波を合成すると、本当に問題の波になるかどうか試してみましょう。どうです？同じになりましたね。

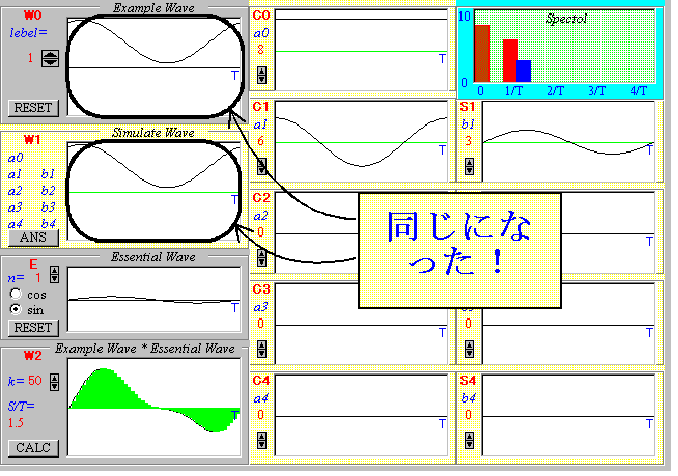
　使用する波の数をlebelボタンで変えたり、波【W0】のRESETボタンを押すことによって問題の波が変わるので、いろいろと試してみましょう。波の形がどんどん変化して、問題の波に一致したときとても感動しますよ。