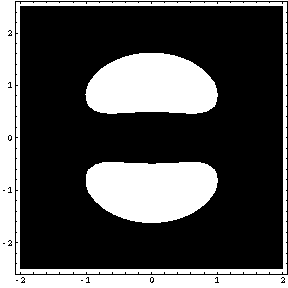ContourPlot

　今度は、3次元図形の断面を探っていきましょう。まず、3次元図形の等高線を描画してみます。使うコマンドは「ContourPlot」です。書式は次のようになっています。

　ここで、Contours は等高線を緯線を何段階に表すか、その回数を表します。それでは、次のような関数の表す図形を考えましょう。右側は、上から見た図です。

f [ x_ , y_ ] := ( x ^ 2 + 3 y ^ 2 ) Exp [ 1 - x ^ 2 - y ^ 2 ]

Plot3D [ f [ x , y ] , { x , -2 , 2 } , { y , -2.5 , 2.5 } ]

Plot3D [ f [ x , y ] , { x , -2 , 2 } , { y , -2.5 , 2.5 } , ViewPoint -> { 0 , 0 , 2 } , PlotPoints -> 40 ]

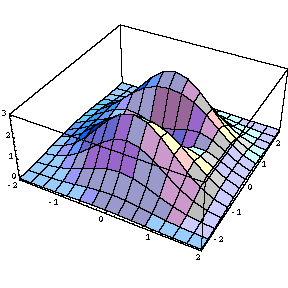
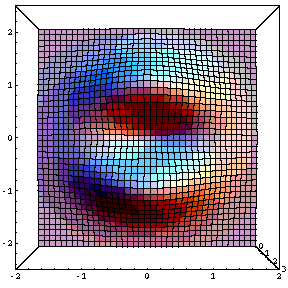
　この図形の等高線の表す図を描画してみましょう。左が15段階、右側が5段階に分割しています。

ContourPlot [ f [ x , y ] , { x , -2 , 2 } , { y , -2.5 , 2.5 } , PlotPoints -> 40 , Contours -> 15 ]

ContourPlot [ f [ x , y ] , { x , -2 , 2 } , { y , -2.5 , 2.5 } , PlotPoints -> 40 , Contours -> 5 ]

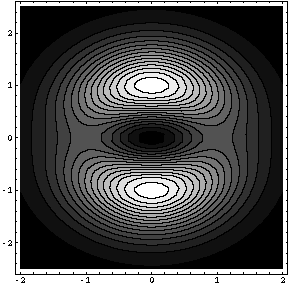
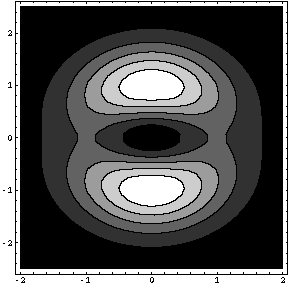
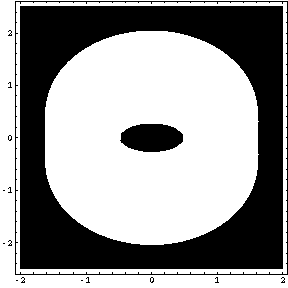
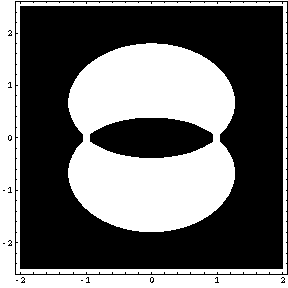
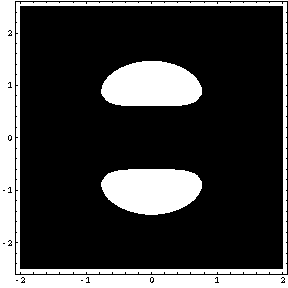
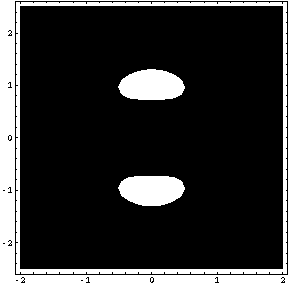
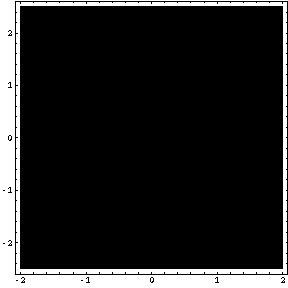
　それでは、「Table」コマンドとオプション「PlotRange」を用いて、方程式 f [ x , y ] = k の表す2次元図形を描画してみましょう。白い部分が解のある部分で、黒い部分が解のない部分です。

Table [ ContourPlot [ f [ x , y ] , { x , -2 , 2 } , { y , -2.5 , 2.5 } , PlotPoints -> 40 , Contours -> 1 , PlotRange -> { k , k } ] , { k , 0 , 3 , 0.5 } ]