ParametricPlot3D

　次に、媒介変数を用いた関数のあらわす図形を描画してみましょう。使うコマンドは「ParametricPlot3D」です。書式は次のようになっています。

　これを用いて、様々な図形を描画させてみましょう。

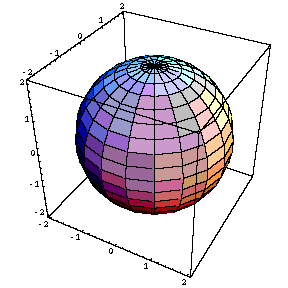
　球面、変形球面（りんご面）

ParametricPlot3D [ { 2 Cos [u] Sin [v] , 2 Sin [u] Sin [v] , 2 Cos [v] } , { u , 0.5 Pi , 2.5 Pi } , { v , 0 , Pi } ]

ParametricPlot3D [ { v Cos [u] Sin [v] , v Sin [u] Sin [v] , v Cos [v] } , { u , 0.5 Pi , 2.5 Pi } , { v , 0 , Pi } ]

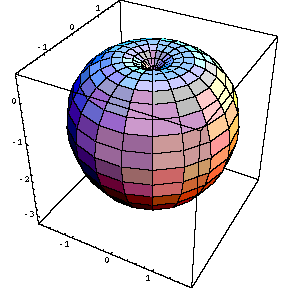
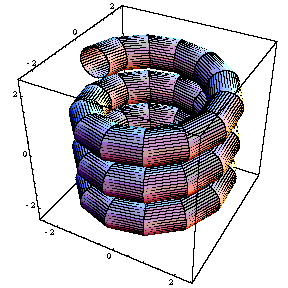
　トーラス、トーラスの変形（コイル上のトーラス）

ParametricPlot3D [ { ( 2 + 0.5 Cos [u] ) Cos [v] , ( 2 + 0.5 Cos [u] ) Sin [v] , 0.5 Sin [u] } , { u , 0.5 Pi , 2.5 Pi } , { v , 0 , 2 Pi } ]

ParametricPlot3D [ { ( 2 + 0.5 Cos [u] ) Cos[v] , ( 2 + 0.5 Cos [u] ) Sin [v] , 0.5 Sin [u] + v / 5 } , { u , 0 , 2 Pi } , { v , -3 Pi , 3 Pi } , PlotPoints -> 40 ]

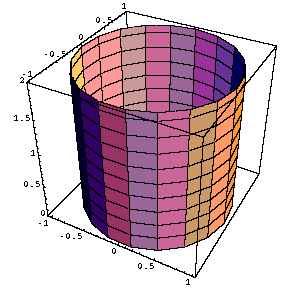
　円柱面、円錐面

ParametricPlot3D [ { Sin [t] , Cos [t] , u } , { t , 0,2 Pi } , { u , 0 , 4 } , PlotRange -> {0,2 } ]

ParametricPlot3D [ { u Cos [t] , u Sin [t] , u } , { t , 0.5 Pi , 2.5 Pi } , { u ,-Pi , Pi} ]

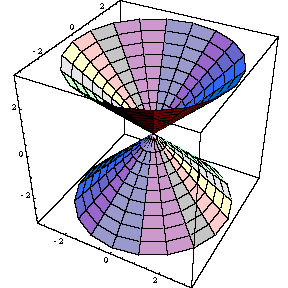
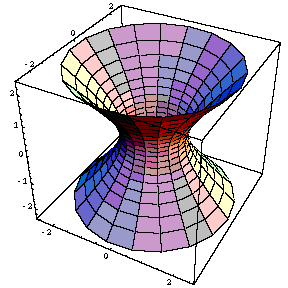
　一葉双曲面、二葉双曲面

ParametricPlot3D [ { Cosh [t] Cos [u] , Cosh [t] Sin [u] , Sinh [t] } , { t , - Pi / 2 , Pi / 2 } , { u , 0 , 2 Pi } ]

fig1 = ParametricPlot3D [ { Sinh [t] Cos [u] , Sinh [t] Sin [u] , Cosh [t] } , { t , 0 , Pi / 2 } , { u , 0 , 2 Pi } , ViewPoint -> { 1.3 , -2 . 4 , 1 } ] ]

fig2 = ParametricPlot3D [ { Sinh [t] Cos [u] , Sinh [t] Sin [u] , - Cosh [t] } , { t , 0 , Pi / 2 } , { u , 0 , 2 Pi } , ViewPoint -> { 1.3 , -2 . 4 , 1 } ] ]

Show [ fig1 , fig2 ]

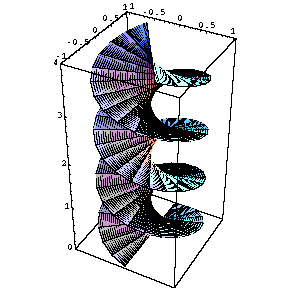
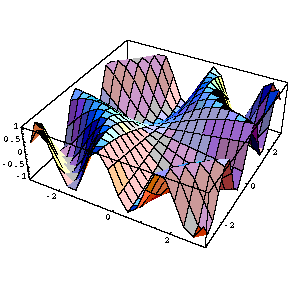
　螺旋曲面、三角関数の作る曲面

ParametricPlot3D [ { u Sin [t] , u Cos [t] , t / 3 } , { t , 0 , 15 } , { u , -1 , 1 } , PlotRange -> { 0 , 4 } , PlotPoints -> 50 ]

ParametricPlot3D [ { t , u , Sin [t u] } , { t , -3 , 3 } , { u , -3 , 3 } ]