| Table |
さて、今度はパラメータを変えて図形の変化の様子を観察してみましょう。使うコマンドは「Table」です。書式は次のようになっています。
| Table [ Plot3D [ g , { x , xmin , xmax } , { y , ymin , ymax } ,{ a , amin , amax , step_a } ] |
これを用いることにより、パラメータの変化にともなう図形を一気に描画させることができます。
それでは 関数 f = x^2+a x y + y^2 が描く図形をパラメータ a の変化ともに観察してみましょう。次のようにinputします。
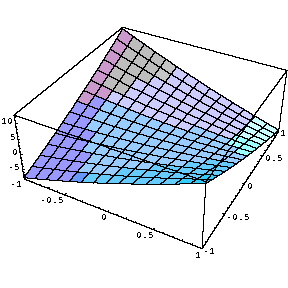
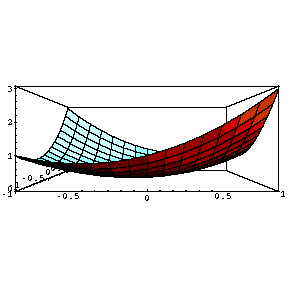
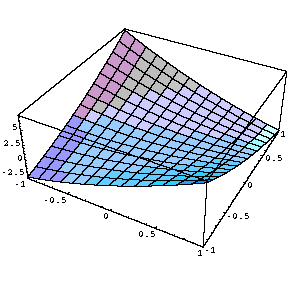
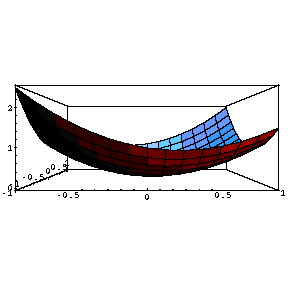
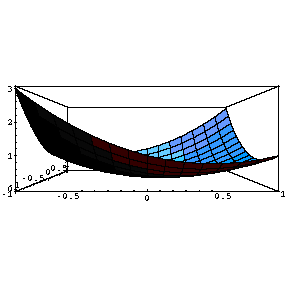
Table [ Plot3D [ x ^ 2 + a x y + y ^ 2 , { x , -1 , 1 } , { y , -1 , 1 } ] , { a ,-1 , 1 , .5 } ]変化の様子を見やすくするために、正面から見た図を右にならべてみます。
Table [ Plot3D [ x ^ 2 + a x y + y ^ 2 , { x , -1 , 1 } , { y , -1 , 1 } , ViewPoint -> { 0 , -2 , 0 } ] , { a ,-1 , 1 , .5 } ]
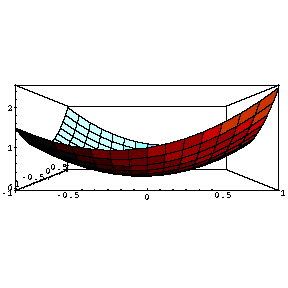
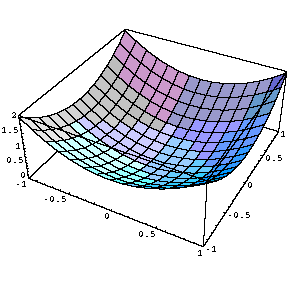
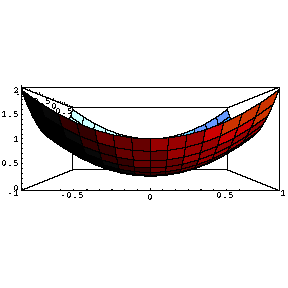
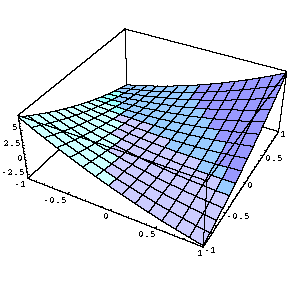
| Do |
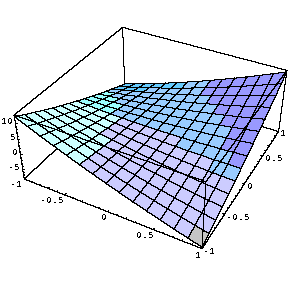
別な関数を用いて描画させてみましょう。陽関数 f(x,y)=SIN(axy) におけるパラメータ a を変化させてみます。
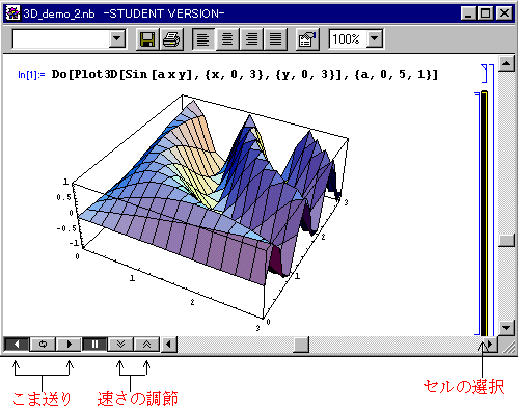
Table [ Plot3D [ Sin [a x y] , { x , 0 , 3 } , { y , 0 , 3 } ] , { a , 0, 5 ,1 } ]
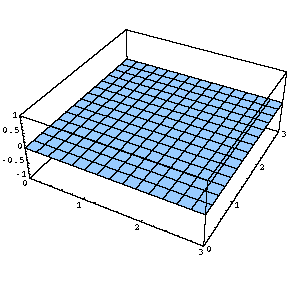
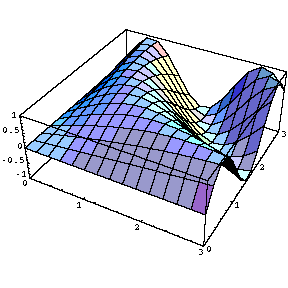
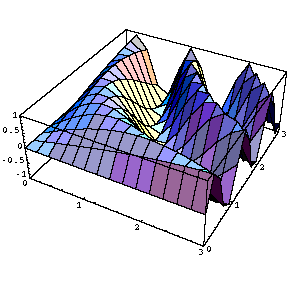
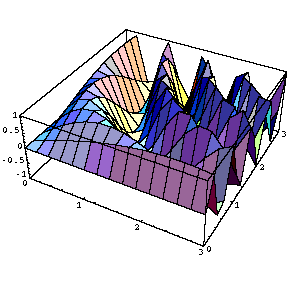
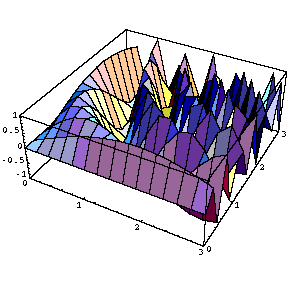
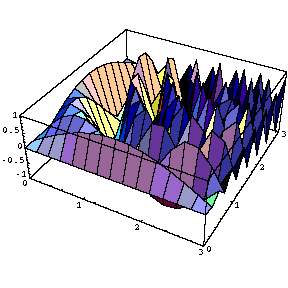
ここで、今作った画像のアニメーションを作ってみましょう。コマンドは「Do」を用います。(「Table」もそのままで使用できるようです。)
D0 [ Plot3D [ Sin [a x y] , { x , 0 , 3 } , { y , 0 , 3 } ] , { a , 0, 5 ,1 } ]次の、要領で実行します。