１．虚円のイメージ化
「x2+y2=-1 て円はどんな円？」
こうした虚円のイメージ化や複素数解のイメージ化は、生徒の興味・関心を引き起こす格好の題材だといえます。
曲線 x2+y2=d は d>0のとき、半径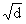
の円を表わしますが、d<0のときは実平面上では表わすことができません。
しかし、世界を実平面から虚平面へと広げることにより、新たな「虚円」の世界が垣間見えてきます。xy平面上に描かれる「実円」上の点 (x，y)を複素数の組と考えれば、新たに2つの次元を構築しなくてはなりません。こうなるとイメージ化することはたやすいことではなくなります。そこでx，yのどちらか一方を複素数と考えて、虚円の世界に少しでも近づいてみましょう。
(1) 実円を持つ場合
円の方程式を
x2+y2=1･･･①
とする。xを実数、yを複素数とし y=u+vi (u，v は実数)･･･② とおく。
①に代入すると
x2+(u+vi)2=1 (x2+u2-v2)+2uvi=1
∴ x2+u2-v2=1･･･③ 2uv=0･･･④
ここで、④の場合分けを③に代入して
u=0 のとき x2-v2=1 (双曲線)
v=0 のとき x2+u2=1 (円)
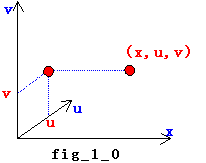
ここまでを3次元空間上のイメージとしてとらえてみます。②で y=u+vi とおくことで新たに虚平面 uv平面を作りました。これと実軸 x とで、3次元の xuv空間を考えることになります（fig_1_0参照）。
③の曲面は一葉双曲面になるが、これと平面 u=0，v=0 とを同時に表わしたのが fig_1_1 です。v=0 のときは、xy(xu)平面上に実円 x2+y2=1 が描かれています。
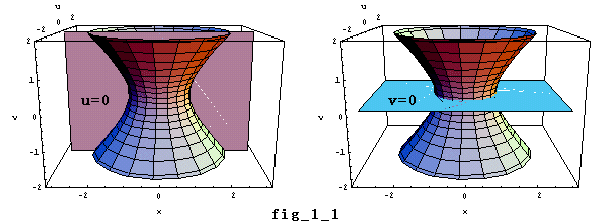
同様にして実円を持たない場合に拡張してみましょう。
(2) 1点になってしまう場合
円の方程式を
x2+y2=0･･･⑤
とする。y=u+vi (u，v は実数)を代入して
x2+(u+vi)2=0 (x2+u2-v2)+2uvi=0
∴ x2+u2-v2=0 (楕円錘面)･･･⑥ 2uv=0･･･⑦
u=0 のとき x2-v2=0 ∴x=±v (2直線)
v=0 のとき x2+u2=0 ∴x=u=0 (1点)
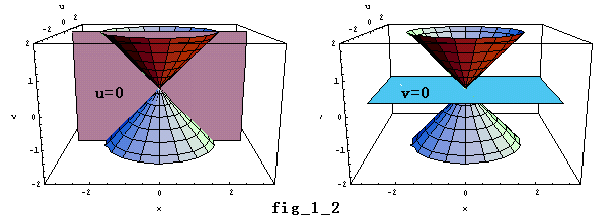
(3) 虚円を持つ場合
円の方程式を
x2+y2=-1･･･⑤
とする。y=u+vi (u，v は実数)を代入して
x2+(u+vi)2=-1 (x2+u2-v2)+2uvi=-1
∴ x2+u2-v2=-1 (二葉双曲面)･･･⑥ 2uv=0･･･⑦
u=0 のとき x2-v2=-1 (双曲線)
v=0 のとき x2+u2=0 これを満たす実数 x,u は存在しない
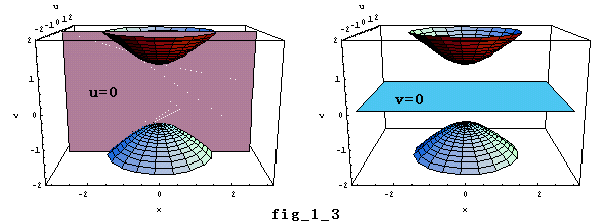
最後の「実数 x,u は存在しない」という部分が、実平面上では円が存在しないということになるのです。
難しいことを展開すると、せっかくの興味・関心や好奇心の目をつんでしまうことにもなります。もっと視覚的にわかりやすく提示することにより、生徒の探求心を伸ばしてあげることも可能となります。