２．2円の交点を通る直線　〜続 Shadow Line〜

　新川高校の中村先生のレポート「Shadow Line その存在性をめぐって」(http://www.nikonet.or.jp/spring/shadow/shadow.htm)のなかで、

と述べられました。

　研究会の中では、虚円の世界をイメージ化させなければ簡単には説明できないのではないか、その虚円のイメージ化をいかに簡単に説明するのか、が大きな問題であるということになりました。

　このことをメーリングリストmatheduの中で投げかけ、いろいろな考えをいただきました。それをまとめたのが「メーリングリスト「mathedu」　その実例から」です (http://www.nikonet.or.jp/spring/m/lml_01_01.htm)。またそれに対して、中村先生から教育学的な立場からのレポート「仮想会議におけるShadow Lineの存在性をめぐって 」(http://www.nikonet.or.jp/spring/shadow/sl_net.htm)も拝見させていただきました。

　しかし、自分の中ではしっかりと消化できずもやもやした気持ちが依然として残っていました。それは「虚円の世界のイメージ化」が自分自身の中でしっかりとなっていなかったためです。もっと直感的に提示できるような、そうしたものが欲しかったからです。

　mathedeの中で愛知教育大学の飯島康之先生が「xy平面を複素化することによって,必然的に4次元になってしまうことが,特に高校生への話題としては,結構厳しいものがある」ということを述べられました。そして、2次方程式の複素数解を触れてから、複素数への拡張に慣れてからがいいのではないか、というようなことも述べられました。

　そして第22回の研究会('97.10実施)で野幌高校の伊藤先生が複素数解のことに触れられ、それに触発されて自分なりにまとめたのがこのレポートと「虚数解のイメージ化」(http://www.nikonet.or.jp/spring/cplx/cplx.html)の2本です。

　さて、先ほどの虚円のイメージ化を用いて2円の交点を通る直線の問題を考えてみましょう。

　簡単のために2つの円を次のようにおきます。

　　C₁：x²+y²=1･･･�@　　C₂：(x-3)²+y²=1･･･�A

　xyの実平面上では、この2円は明らかに交わりません。しかし、�@−�Aより、x＝3/2 という解?が得られます。この直線？ x＝3/2 というのはどういった意味を持つのでしょう。

　先ほどと同様に、xを実数、yを複素数とし y=u+vi (u，v は実数)　とおき�@と�Aに代入してみます。

　�@に代入すると、

　　x²+(u+vi)²=1　　　(x²+u²-v²)+2uvi=1

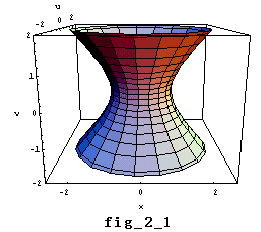
　　　∴ x²+u²-v²=1･･･�B　(一葉双曲面)

　　　　 2uv=0･･･�C　(2平面)

　　u=0 のとき　　x²-v²=1　(双曲線)

　　v=0 のとき　　x²+u²=1　(円)

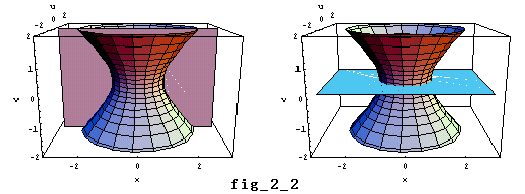
　ここで�Bの曲面が fig_2_1 です。この曲面と 2平面 u=0，v=0 とを描いたのが次の fig_2_2 となります。虚平面と実平面とに現れる図形が見てとれます。

　同様に�Aに代入すると、

　　(x-3)²+(u+vi)²=1　　　(x²-6x+9+u²-v²)+2uvi=1

　　　∴ (x-3)²+u²-v²=1･･･�D　(一葉双曲面)

　　　　 2uv=0･･･�E　(2平面)

　　u=0 のとき　　(x-3)²-v²=1　(双曲線)

　　v=0 のとき　　(x-3)²+u²=1　(円)

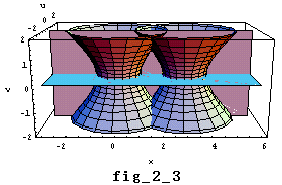
　2つの曲面と2平面を同時に描画したのが、fig_2_3 です。平面 v=0 (xu(y)平面)ではもともとの実円 C₁とC₂ が描かれますが、明らかに交わっていません。しかし、yが虚数であるとき、xv平面上には双曲線が広がっていきます。

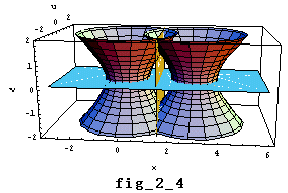　この双曲線の交点の影が、x軸上に2円の差として作られる"平面" x=3/2 の一部として、"直線" x=3/2 が浮かび上がってくることがわかります。(fig_2_4 参照)
　このように中村先生の示したとおり「虚数の軌跡によって作られる曲線の影のようなもの」としての存在が垣間見えました。結局は、3次元空間における曲面のイメージ化、が大きな問題だったのかもしれません。ここに載せた図はすべて「Mathematica 3.01」を用いて作成しました。また、コンピュータに助けてもらったという感じです。

　しかし、x,y両方を複素数とした場合のイメージ化という課題が残ります。また、「Shodow Line」のあとがきで提起されている、2つの曲線の交線を通る曲線群への一般化、すなわち、

　　k･f(x、y)+l･g(x、y)=0

への適用などまだまだ未知の分野が多いといえます。見えずらい世界への挑戦が必要でしょう。