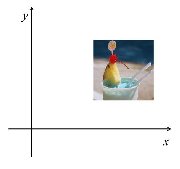
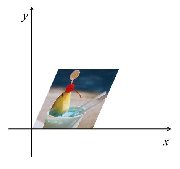
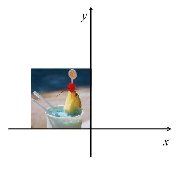
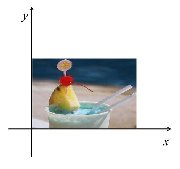
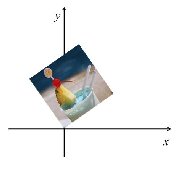
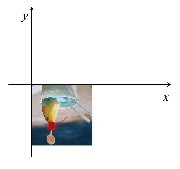
 次のa〜fは,2次元図形の幾何変換についての式である。各式の表す変換の内容を解答群Aから,また右の画像にa〜fの変換を施した図を解答群Bからそれぞれ選び,記号で答えよ。 次のa〜fは,2次元図形の幾何変換についての式である。各式の表す変換の内容を解答群Aから,また右の画像にa〜fの変換を施した図を解答群Bからそれぞれ選び,記号で答えよ。ただし,変換前の座標をx,y,変換後の座標をx’,y’とする。
【解答群A】 オ.平行移動 カ.鏡映(x軸対象) 【解答群B】
|
数学分野におけるグラフの移動(数Ⅰ)や1次変換(数C)に関する問題です。数学では数式として扱うことが多いのですが,「情報」のように画像の変換として取り扱うことで,より具体的でイメージのつかみやすい題材となります。
次のところにWeb上で体験できる1次変換のページがあります。参考にしてみてください。
⇒「Javaで1次変換」
http://www.nikonet.or.jp/spring/transfer/transfer.html
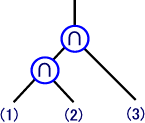
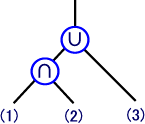
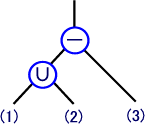
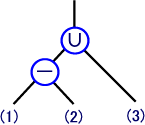
| 次のa〜cの立体は,解答群Bの6個のプリミティブのうちの3個の集合演算からできている。このとき,それぞれに対応する演算を解答群Aから選び,また該当する(1)〜(3)のプリミティブを解答群Bから選べ。 ただし,∩は積集合,∪は和集合,−は差集合を示し,差集合の場合は,左側の立体から右側の立体を引くことを意味するものとする。
【解答群A】
【解答群B】
|
数学の集合に関する問題です。CGではCSG(Constructive Solid Geometry)といって,基本的な物体(プリミティブ)を和集合,積集合,差集合といった演算で組み合わせて形状のモデリングをする基本的なテクニックです。
数学では要素を用いて机上で行いますが,集合演算をイメージ化する点では有効な方法といえます。3個の集合のベン図を3次元グラフィックスでイメージ化したものが「数学玉手箱」にありますので,参考にしてください。
⇒「数学玉手箱 3次元グラフィックスで見るベン図」
http://www.nikonet.or.jp/spring/sanae/MathTopic/MathTopic.htm
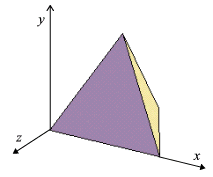 下の表は,右の正四面体における頂点の座標の情報をまとめたものである。空欄ア〜ウに数値を入れよ。
|
数学の題材そのものであるが,CGにおいても空間における3次元形状の座標を正しく理解することが必要となります。数学における座標系と違うので違和感を覚えるかもしれませんが,座標系についてもしっかりと把握することが大事です。
「LiveGraphics3D」(by Martin Kraus)を用いた授業実践の資料が,次のページにありますので参考にして下さい。
⇒「空間図形の導入部分におけるコンピュータの活用」
http://www.nikonet.or.jp/spring/My3D/My3D.htm
次のa〜cの立体を平面で切断するとき,現れる断面の形状をそれぞれ解答群より選べ。
【解答群】
|
数学においては古典的な問題ですが,生徒にとっては苦手な分野です。CGにおいても,切断面がどのような形状になるかをイメージすることは,とても重要になります。
次のページに立方体の11全ての切断図と展開図がのっていますので,参考にして下さい。
⇒「数学玉手箱 立方体の展開・切断」
http://www.nikonet.or.jp/spring/sanae/MathTopic/MathTopic.htm
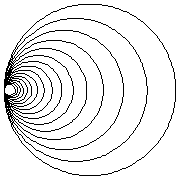
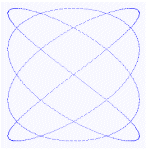
次のア〜カの図形に関係のある事柄を解答群から選べ。
d.等比数列 e.周期関数 f.MOD関数 |
数学で用いられる様々な関数や数列などは,デザインへ応用されることが多いといえます。この他にもフラクタルや模様の敷き詰めなど,現代数学に関わる分野はコンピュータデザインには欠かせない分野です。
次のア〜カの図形に関係のある人物名を解答群から選べ。
d.ベジェ e.コッホ f.シェルピンスキー |
数学の中にあらわれる色々な曲線や図形は,前の例題と同様CGデザインへ応用されることが多いといえます。そうした図形の中には人の名前を付けて呼ばれているものが色々とあります。
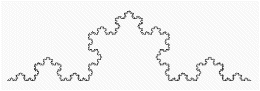
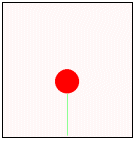
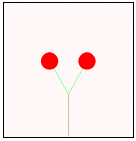
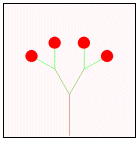
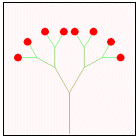
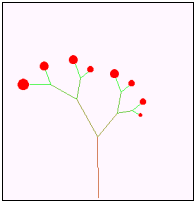
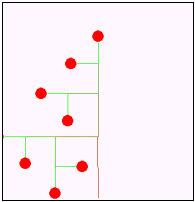
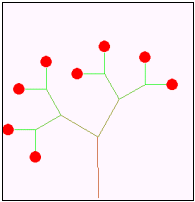
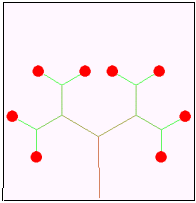
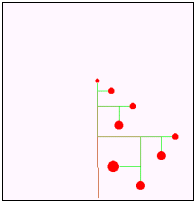
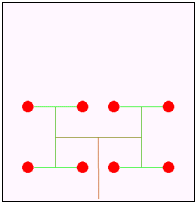
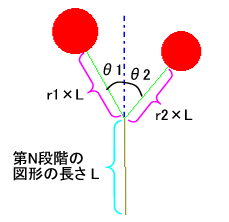 以下の文章は,形の法則性について述べたものである。次の生成手順に従い,a〜dの条件を用いて生成される第4段階の図形として最も適するものを解答群から選べ。 以下の文章は,形の法則性について述べたものである。次の生成手順に従い,a〜dの条件を用いて生成される第4段階の図形として最も適するものを解答群から選べ。【生成手順】 第1段階は単位長さの水平成分で表した1本の枝に実がなっている。N+1段階では第N段階の先端に新しい枝を,右図のように長さの比率と角度を決めて作成する。
【解答群】
| |||||||||||||||||||||||||||||||||||||||||||||||||
至る所で屈曲している自己相似な図形をフラクタル図形といいす。しかし,自己相似ではありませんが,再帰的に描かれる図形は他にもあります。そんな図形の一つがこの「樹木曲線」です。形の法則性を用いることで,植物などの形状を生成する場合に有効です。
次のページでは,この樹木曲線をインタラクティブに体験できます。
⇒「Javaでものみながらふらくらるたいむ」
http://www.nikonet.or.jp/spring/Fractal/Fractal.htm