 | 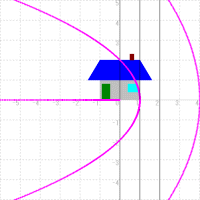 |  |
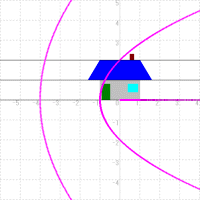
| 水平な直線を変換 | 垂直な直線を変換 | 変換された直線を合成 |
変換 w=z2 を例にとって考えてみましょう。z=x+yi とします。次の図のように,家の図の横の線を作っているy=0,1,2の3本の直線を変換して見ます。同様にx=-1,0,1の3本の直線も変換します。
すると原点を焦点,実軸を軸とする放物線が現れてきましたね。実は今まで直線で書かれていた図が,今度は放物線にそって描かれていくことになるのです。ここでx=-1,0,1の3本を変換したときに曲線が2本しか現れないのは,x=-1とx=1の変換された曲線が同じためです。
 |  |  |
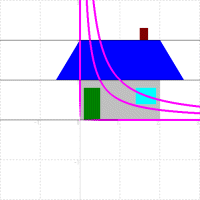
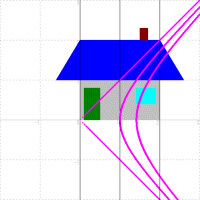
| 水平な直線を変換 | 垂直な直線を変換 | 変換された直線を合成 |
○ w=√z の場合
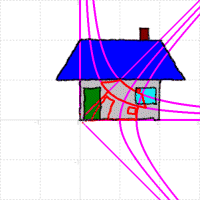
次の図のように,実軸に平行な直線は,x軸,y軸を漸近線とする直角双曲線にうつされます。また実軸に垂直な直線は,今の直角双曲線を原点の周りに-45°回転させたものになります。
 |  |  |
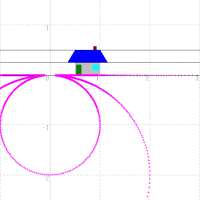
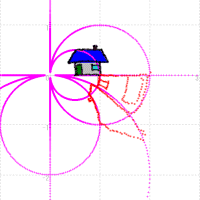
次の図のように,実軸に平行な直線は,y軸上に中心と直径を持つ円にうつされます。また実軸に垂直な直線は,x軸上に中心と直径を持つ円にうつされます。
 |  |  |
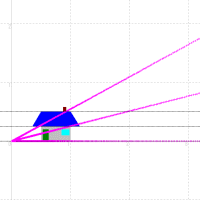
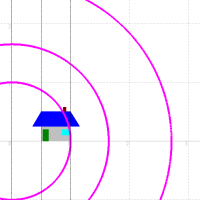
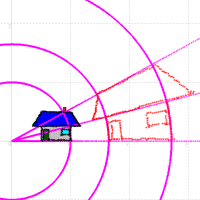
次の図のように,実軸に平行な直線は,原点を通る直線にうつされます。また実軸に垂直な直線は,原点に中心を持つ円にうつされます。
 |  |  |