５．座標平面全体の変換
様々な図形を複素変換してきましたが，次に平面全体を変換するとどうなるでしょうか。実軸に平行な直線と垂直な直線全体を変換してみるのです。次の図は w=z2 で変換したものです。
先ほど見たように，原点を焦点とし，実軸を軸とする放物線の集合となっていますね。
 |
⇒ |
 |
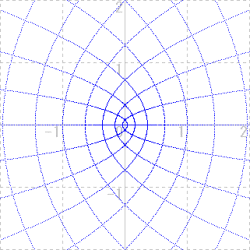| 平面全体を w=z2 で変換 |
それでは他の変換ではどうでしょう。代表的なものを見てみましょう。
 |
|
 |
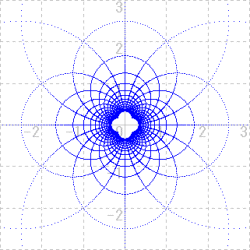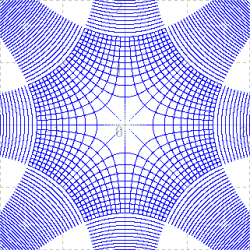| w=1/z の変換 |
|
w=√z の変換 |
 |
|
 |
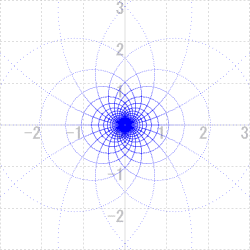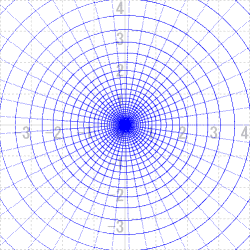| w=1/z2 の変換 |
|
w=ez の変換 |
これらの複素変換の特徴は，任意の2つの曲線のなす角が変換後も等しく保たれているところです。2つの曲線のなす角とは，交点でそれぞれの曲線に接線を引いたとき，その接線のなす角をいいます。この様な変換を「等角写像」といいます。
直行座標を変換したので変換後の曲線のなす角は，どれも90°になっていますね。
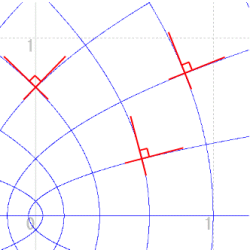
しかし全ての点で等角かというと，そうではありません。右の変換は w=z2 ですが，原点においては90°ではなく，180°に写っています。
