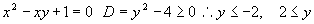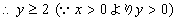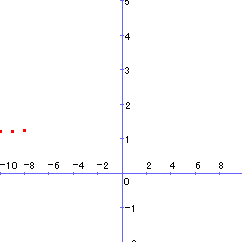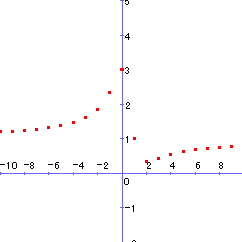xが実数のとき,関数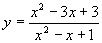 の最大値,最小値を求めよ。 の最大値,最小値を求めよ。 |
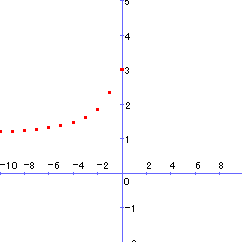
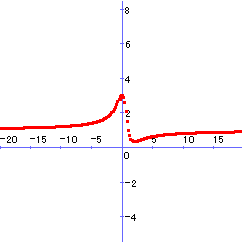
普通,最大・最小と言えば,グラフを描いて調べるが,その方法が使えない。数Ⅲまで履修しても,なかなか面倒なグラフです。一見しただけでは,連続かどうかも定かではない。
そこで登場してくるのが,xの実数条件です。しかし,生徒にとってはあまりに唐突であり,受験のためのテクニックを身につけたからといって,内容まで理解しているものは少ないのではないでしょうか。そこで,基本に戻って点をプロットして,グラフの概形を知ってみよう。イメ-ジを膨らませてみることは非常に有効です。確かに最大,最小はありそう。しかし,どうして実数条件なるものがでてきたのでしょうか。確かにxは実数ですから,その条件は必要ですが,果たしてそれだけで十分なのでしょうか。それなら,今までの最大,最小問題も実数条件で解けるか。
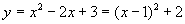 最小値は x=1 のとき y=2
最小値は x=1 のとき y=2
式を変形して,実数条件を用いると 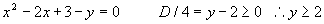
では 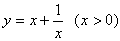 に相加・相乗平均を用いない場合
に相加・相乗平均を用いない場合