コーヒーカップの描く軌跡�A　〜大円盤・中円盤を動かす〜

　さあ、早速調べていくことにしましょう。手当たり次第ランダムに変化させても規則性を見つけるのは大変なので、まずは大･中･小3枚の円盤のうち、大円盤と中円盤の二つを動かしてみましょう。次のサンプル例の図の左上に表れている数字が、3つの円盤の角速度をあらわしています。

回転する速さの比が整数の場合

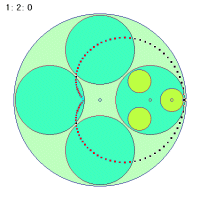
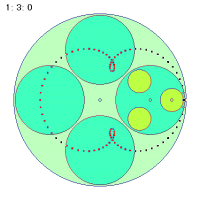
　2つの盤の回転比が問題になりますから、大円盤の比をいつも1に固定して考えましょう。こうした状態で中円盤、すなわちコーヒーカップが乗っている盤の速さを変えてみます。シミュレートした結果の一部を次にあげてあります。

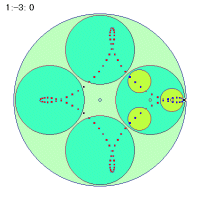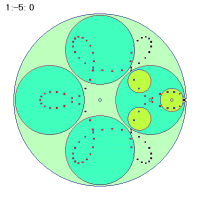　まず、中円盤の角速度が正か負かによって、軌跡の形が違ってくるのがまず目につきます。正の場合は外側から、負の場合は内側から折り返していきます。そして折り返しの分岐点の数が、正の場合は角速度の数値より1少なく、負の場合は1多いことに気づきます。

回転する速さの比が簡単な小数の場合

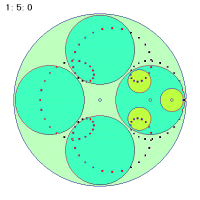
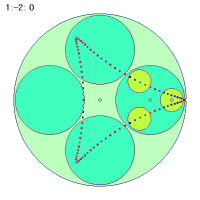
　次に中円盤の回転比が簡単な小数の場合を考えてみましょう。いくつかのサンプル例を考察してみます。

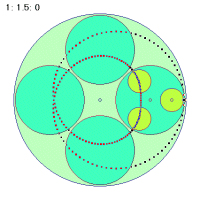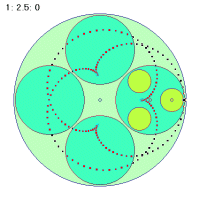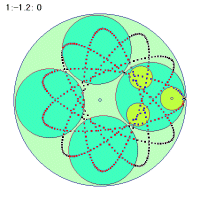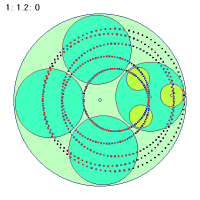
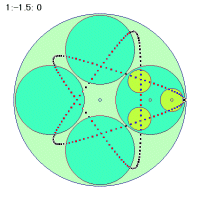
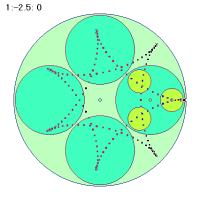
　最初の角速度1.5と2番目の2.5の場合は2秒間での軌跡を、3番目の1.2の場合は5秒間での軌跡を描いています。よく見ると2秒間で1個と3個、5秒間で1個の折り返し点ががあります。

　このことから，やはり先ほど考察したことが小数の場合でも当てはまることがわかります。同様のことが角速度が負の小数の場合にもいえます。

折り返し点の秘密？

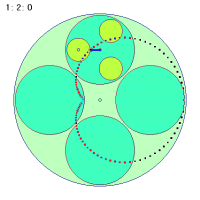
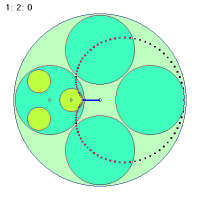
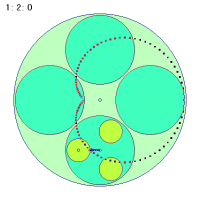
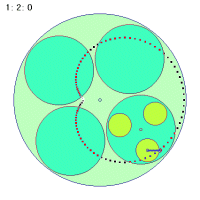
　なぜこのような事が起こるのか、その折り返し点に関わる秘密を探ってみましょう。次の図は大円盤が一回転する間に中円盤の中心とカップに乗っている人間とのベクトルを矢印で示したものです。中円盤が回転しなくても、中円盤は大円盤に引きずられて一回転します。しかし、中円盤が一回転してもループの半径が変わるだけで同じく一回転しかしません。

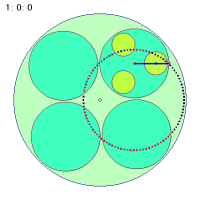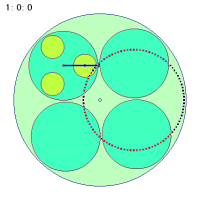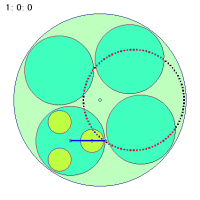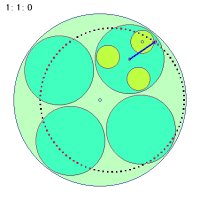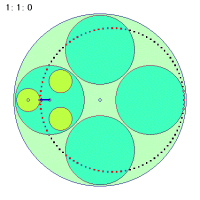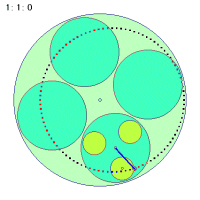　これに対して（1秒間に）2回転する場合は0.5秒ですでにすでに一回転するわけですから、そこで折り返しがつくことになります。結局秘密でもなんでもなくて、ごく当たり前のことだったわけです。中円盤の回転数が負の場合も同様にして考えられそうです。
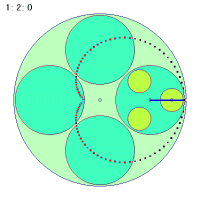
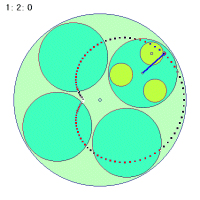