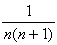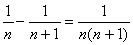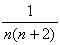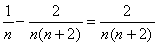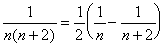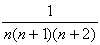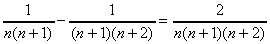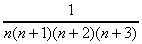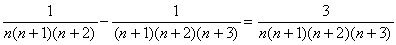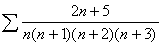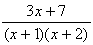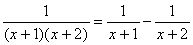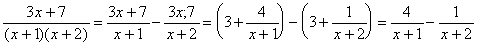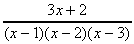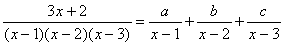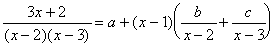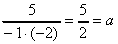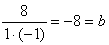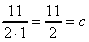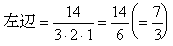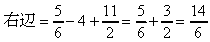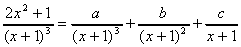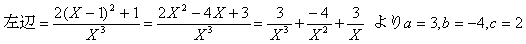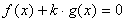授業の中では、分数式をまとめて教えることをしてきませんでしたが、数Aの数列の和の分野で部分分数に変形するときに、必要性を感じました。教科書では、分数式を扱わずに説明していますが、授業では文字式の入った計算で教えました。分数式という言葉は数Ⅲの範囲、ましてや分数式の恒等式で初めて出てくる内容ですが、他の分野でも、様々な問題を解く過程で分数式の計算が必要になるときが多くありました。
例1
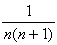 を部分分数に分解せよ。 を部分分数に分解せよ。
|
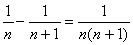 となるからできあがり。
となるからできあがり。
例2
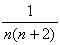 を部分分数にせよ。 を部分分数にせよ。
|
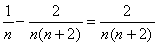 となるから両辺を2で割って、
となるから両辺を2で割って、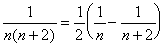
例3
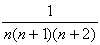 を部分分数にせよ。 を部分分数にせよ。
|
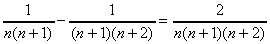 となるから両辺を2で割って
となるから両辺を2で割って
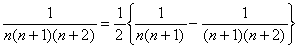
例4
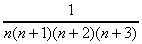 を部分分数にせよ。 を部分分数にせよ。
|
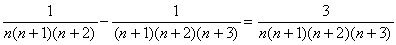 となるから両辺を3で割って
となるから両辺を3で割って
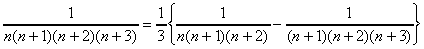
例1~例4を通して、分母の最後と最初を除いたものを分母とする分数の差を考えるというイメージを持たせたかったのですが、おおむね成功したように思えます。
これは、次のように発展していきます。(しかし、これは難問といえるので、このような例を利用する数列の問題は教えてはいません。)
例5
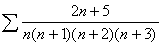 を求めよ。 を求めよ。
|
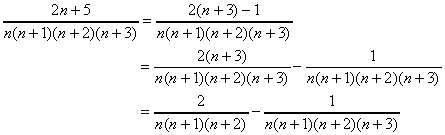
より、前の項と後ろの項を部分分数にして和を求める。(以下省略)
また、この簡易な部分分数の変形は、数Ⅲの積分では、次のように発展させるつもりです。これも、現3年生にはまだ教えていません。
例6
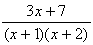 を部分分数にせよ。 を部分分数にせよ。
|
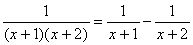 より、両辺を3x+7倍して
より、両辺を3x+7倍して
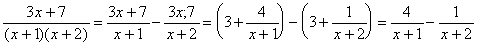
あるいは
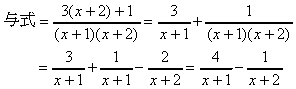
分数の恒等式は、特に積分の時に有効であり、その他の場合にはあまり使われないのですが、数値代入法が消えたのは残念なことです。上の例6のようにできない場合があるからです。
例7
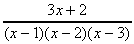 を部分分数にせよ。 を部分分数にせよ。
|
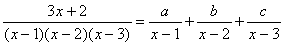 とおく。
とおく。
両辺をx-1倍すると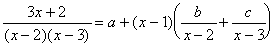 となる。
となる。
x=1を代入すると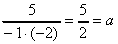
以下同様に
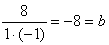 (指で左辺のx-2を隠しながらx=2を代入する)
(指で左辺のx-2を隠しながらx=2を代入する)
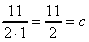 (指で左辺のx-3を隠しながらx3を代入する)
(指で左辺のx-3を隠しながらx3を代入する)
よって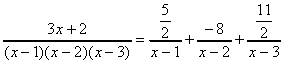
逆に、これは全てのxに対して成立する。
などと書いて、実はx=4を代入すると
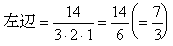
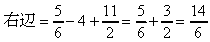 で吟味
で吟味
次の例は、恒等式では有効な方法として知られているものですが、機会を見て教えていこうと思っています。
例8
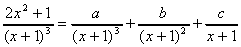 を満たすa,b,cを求めよ。 を満たすa,b,cを求めよ。
|
X=x+1とおくと、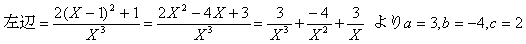
これらの分数の式の取り扱いについては、早いうちに慣れさせておく方がよいように思います。現在では、1年生の数と式(数A)で、分数式の計算や、分数式の恒等式を教えています。例えば文字の入った連立方程式を解くというのは、教科書では数Cの行列あたりで取り扱っていますが、実際はそれ以前に何度かこういった計算が出てくるのです。現3年生は旧課程の生徒に比べて、分母が0になるという場合分けをする意識が低いように思えました。
|
例9 直線ax+y=-a と x-ay=1 において、aが全ての実数値を取って変化するときに、この2直線の交点の軌跡を求めよ。(数Ⅱ)
|
aを消去するときに、分母に文字がくることになります。しかし、分数式の学習が不十分で、場合分けをしないために答えが円全体になってしまうのは、以前にも生徒がよくやる間違いですが、新課程の生徒に間違いが増えたと感じています。
また、別解として直交性を利用する方法もありますが、教科書では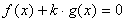 のグラフがg(x)=0自身を表さないことを明確に述べていないために、点を除くことができないものが多いと思います(これは、別の問題ですがグラフのイメージもかなり弱い感じがします)。
のグラフがg(x)=0自身を表さないことを明確に述べていないために、点を除くことができないものが多いと思います(これは、別の問題ですがグラフのイメージもかなり弱い感じがします)。
 分数式について
分数式について