 無理式について
無理式について
例えば、距離や2次方程式の解の公式の絡む問題では、√が出てきますが、無理式の取り扱いを学んでいないために同値を考えずに計算して間違えます。√についてはある程度知識があるだけにあまり怖がらずに計算してしまって間違えてしまうのです。生徒の中に次の例の解法のように解くのもいました。初めて解く生徒にはたぶん難しいといえるので、成績上位の生徒が、苦労して編み出した方法であろうと思います。それを他の生徒がまねて、クラスの半数以上の生徒が同じ解き方をしていました。授業ではその生徒の考え方の正しさと計算の不確かさを教えましたが、この考え方をむしろ育てたいと思いました。
実数解を持つから、判別式 D=a2-4a=a(a-4)>0 よってa<0,4<a…①
数学の解としては同値が気になります。無理方程式を代数的に解くというのは、同値についての意識を持たせるにはよい教材ですので、無理関数等を数Ⅲで学び、しかも幾何的な解法で終始するのは残念なことです。
授業では「2乗すると答えが増える(かもしれない)ぞ、x=2はx2=4になると解が増えるだろう。2乗したら増えたかどうかはチェックしないとだめだ。」などといっております。(2乗すると実は解が減る場合もあるのですが)
例9の解法として2つの式を2乗して加えると、
例10 x2+ax+a=0が1より小さな2つの実数解を持つときに、aの値の範囲を求めよ。
解を求めると 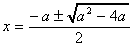
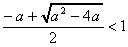
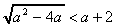
両辺を2乗して
などというのは、間違いであるというのはわかるが、どこで間違えているのか説明しにくいと思います。