 数Bと融合された微分積分について
数Bと融合された微分積分について
数Ⅱの微分は3次式まで、積分は2次式までであるのは、因数定理を数Bで学ぶために3次方程式が解けないからだと思われます。とすると数Ⅱと数Bの関連のある問題はどこで取り扱って教えていますか。このあたりは次のような面白い性質があります。授業や補習ではこのような入試問題によく見られる2次関数や3次関数の問題を取り扱いました。
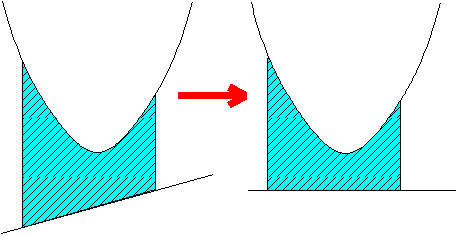
これは2つのグラフの間に並んだ竹ひごの面積を考え、y=dx+eをx軸に重ねた時に面積が同じになるというイメージで説明できます。2つのグラフの同じxの値に対するy座標の差を変化させないような変換ととらえます。
(1)2次関数y=ax2+bx+cと1次関数y=dx+eに挟まれた部分の面積は y=(ax2+bx+c)-(dx+e)とx軸にはさまれた部分の面積に等しい。
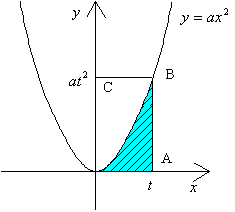
(2)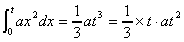 より図の斜線部分は長方形OABCの1/3の面積である。 より図の斜線部分は長方形OABCの1/3の面積である。
|
((2)の図形的なアイディアは 札幌藻岩 菅原 満 先生が数実研で発表されたものです)
(3)y=ax2と同じ形の放物線y=f(x)とy=g(x)とこれらの共通接線y=dx+eによって囲まれる部分の面積は、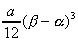 である。 である。
|
これは、(1)と同様にy=dx+eをy=0に変換させたときに図のようになり、それぞれの接点をα、βとするときに、グラフより明らかに左右対称であるから左右の面積は等しくなり(2)によって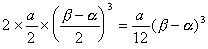
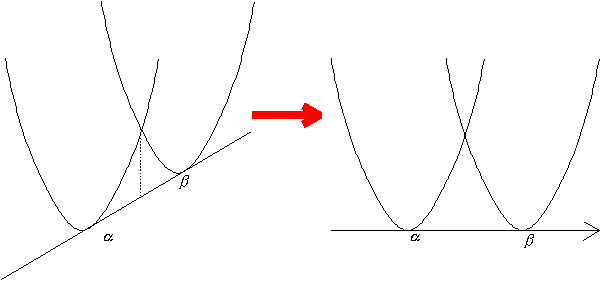
| 例11 y=x2+2x+3とy=x2-4x+15とこの2つの放物線の共通接線によって囲まれる部分の面積を求めよ。 |
x2+2x+3=x2-4x+15よりx=2。
それぞれの放物線の軸はx=-1,x=2。
よって左の接点のx座標はx=1/2・・・(*)。ここでの接線はy=3x+11/4となる。
また面積は、1/12・33より9/4である。
(*) 各々の頂点のx座標をT1,T2、接点のx座標をP1,P2とするとき、T1T2=P1P2=3 かつP1P2の中点のx座標は2であるから、Pのx座標は 2-3/2=1/2、P2のx座標は2+3/2=7/2
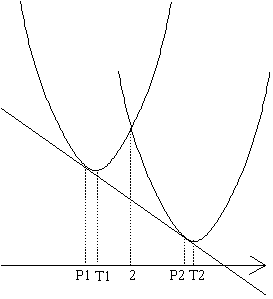
(4)y=ax2と同じ形の放物線y=f(x)に点Pから2本の接線が引けるときに、左右の面積が等しくなり 合計で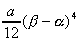 となります。 となります。
|
これは、放物線と右の接線を(1)によって変換し、次に左の接線と放物線を(1)によって変換すると、図のようになり、上の(3)と同値になるからです。この時、Pのx座標は2つの接点の中点になることもわかります。
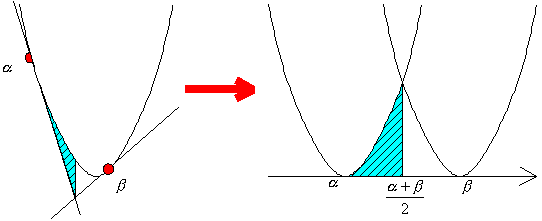
| 例12 y=x2+2x+4 に原点より引いた2本の接線とこの曲線によって囲まれた図形の面積を求めよ。 |
接線をy=axとすると x2+(2-a)x+4=0 が重解を持つことから、 a=-2,6
このとき x=-22,2 よって面積は 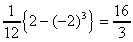
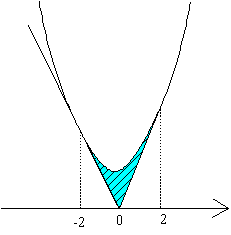
また、授業では取り扱っていませんが、次の2つの性質も、同様の変換によって証明されます。
| (5)y=ax2と同じ形の放物線y=f(x)に接線が引けない点P(m,n)を通る直線と、放物線によって囲まれる面積が最小となる最初となる時の直線の方程式は、 y=f'(x)(x-m)+n である。また、交点の中点がP(a,b)となっている。y=ax2と同じ形の放物線y=f(x)に接線が引けない点P(m,n)を通る直線と、放物線によって囲まれる面積が最小となる最初となる時の直線の方程式は、 y=f'(x)(x-m)+n である。また、交点の中点がP(a,b)となっている。 |
a>0とする x=m に対応する曲線上の接線によって変換し、さらに、頂点が原点にくるように平移移動すると、PはP'(0,t) ただしt>0に移されたとして良い。P'を通る直線をy=kx+tとし、ax2-kx-t=0の解をα、β(α<βとするとき
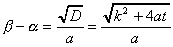
これをもとのグラフに逆変換する。
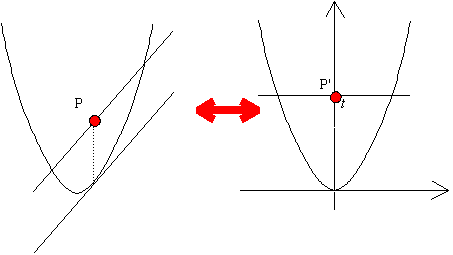
| (6)直線と放物線の交点をS、QRの中点をPとすると、PSはy軸に平行で、その中点は放物線上にある。 |
y軸に平行であることは前に述べたことから明らか。
後半は、変換して p'(0,aα2),Q'(α,-aα2)とするとQ'での接線は、y=2aαx-aα2であるからx=0のとき、y=-aα2。よってP'S'の中点は、放物線上にある。
これを逆に変換すると良い。
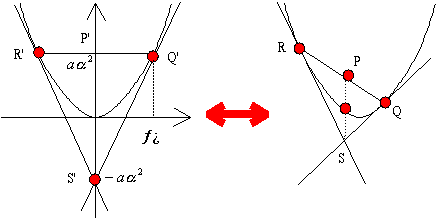
| (7)P(m,n)より放物線y=f(x)に2本の接線が引けるときに、その接点を結ぶ直線は、y=f'(m)(x-m)+(2f(m)+n)である。P(m,n)より放物線y=f(x)に2本の接線が引けるときに、その接点を結ぶ直線は、y=f'(m)(x-m)+(2f(m)+n)である。 |
これは、上の(5)(6)より明らか。
この性質を使うと、例12はy'=2x+2より(0,8)を通る割線(極線)を考えると、Y=2x+8となるから、x2-2x-8=0を解くと接点がわかることになります。
以上の証明は、極めて視覚的なものですが、代数的に解くことも出来ます。しかし、ワープロで数式を書くのが苦手であるし、数式の羅列はつまらないので記載しないことにします。
例えば、 (6)は次のように証明されます。
y=ax2+bx+cとする。接点PQのx座標をα、βとするときに、それぞれの接線は
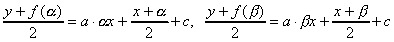
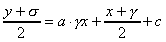
x=γのときのyの値をYとすると、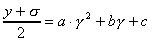
3次関数についても次のような性質があります。
| (1)整関数y=f(x)のx=aにおける接線は、(x-a)2で割った余りである。 |
f(x)=(x-a)2Q(x)+bx+cとすると、y=bx+cとの連立方程式は明らかに、x=aを重解に持つから、y=bx+cはx=aを重解に持つから、y=bx+cはx=aにおけるy=f(x)の接線である。
| 例13 y=x3+3x+1上の点(1,5)における接線の方程式を求めよ。また、その接線が再びこの曲線と交わる点の座標を求め、曲線と接線によって囲まれた部分の面積を求めよ。 |
x3+3x+1=(x-1)2(x+2)+6x-1より接線はy=6x-1、交点は(-2,-13)。面積は{1-(-2)}4/12=27/4。
| (2)整関数y=axn+…+bx+cのx=0における接線はy=bx+cである。 |
これは(1)のx=0における場合となっています。
| (3)2次関数y=ax2+bx+cのbの符号は、x=0における接線の傾きによって決定できる。 |
|
例14 次の2次関数について、a,b,cの符号を決定せよ。
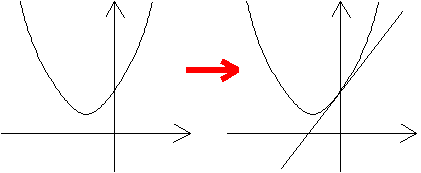 |
上の図よりb>0。
数Ⅰではすでに2次関数と1次関数の共有点を、連立方程式で解くことによって求めるということをさせているので、y=ax2+bx+cとy=bx+cの連立方程式を解くことによって、y=bx+cがx=0における接線であることを教えています。
| (4)3次関数上の点Pにおける接線が再びこの曲線と交わる点をQ、変曲点をRとすると、PRのx座標の差とQRのx座標の差の比は1:2である。 |
これと、次の(5)とあわせると、図の平行四辺形は全て合同ということになります。
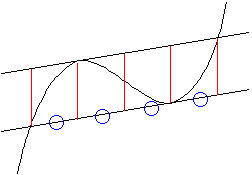
y=ax3+bx2+cx+dにおいてx=αにおける接線をy=lx+nとおく。y''=6ax+2bより変曲点はx=-b/2a。
ax3+bx2+(c-1)x+(d-m)=0は2重解αと他の解βを持つから、解と係数の関係より
これは、(1)による解法がわかっていれば、必要のない性質です。
例11では、変曲点のx座標はy''=6x=0よりx=0。よって交点はx=-2となります。
| (5)3次関数は変曲点に関して点対称である。 |
| 例15 y=x(x-1)(x-3)とy=axが異なる3点で交わり、この曲線と直線で囲まれる2つの部分の面積が等しいときに、aの値を求めよ。 |
y''=6x-8 より変曲点は 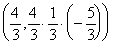
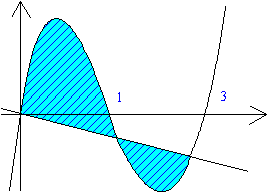
| (3)3次関数fの変曲点での接線gの左右の領域の点からは、この3本の接線が引ける。f及びg上の点からは2本の接線が引ける。fとgの上下の領域からは1本の接線が引ける。 |
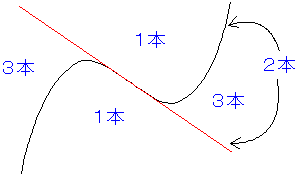
| 例16 点(1,a)からy=x3-xへ3本の接線が引けるようにaの値の範囲を決定せよ。 |
変曲点はy''=6x=0より(0,0)。
ここでの接線はy=-xであるから、(y-x3+x)(y+x)<0に(1,a)を代入してa(a+1)<0 ∴-1<a<0
このような問題は、旧課程では基礎解析の範囲でしたが、新課程では融合問題として扱われることになるのでしょうが、授業では意識して取り上げるようにしました。中には数値を入れた問題を解かせ、性質を述べるだけにとどまったものや、全く教えていないものもありますが、こういった性質を述べることにより、2次関数やグラフに興味を持ってくれたらと思います。
このような性質を使って解くのは、成績下位(楽に答えを出したい)と成績上位者(計算が面倒である)に多く、成績中位者は吟味に使っているようです。