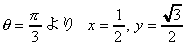 攠夘曄悢偵偮偄偰
攠夘曄悢偵偮偄偰
丂條乆側妏搙偐傜暔帠傪峫偊傞偙偲偑偱偒傞偲偄偆偙偲傪偄偆偨傔偐丄偨偔偝傫偺嵗昗宯傪嫵偊傞偙偲偵側偭偰偄傑偡丅摿偵儀僋僩儖丄暋慺悢丄嬌嵗昗傪捠偟偰丄捈慄偲墌偑壗搙傕弌偰偒偰偄傑偡偑丄惗搆偵偲偭偰偼丄寢嬊偼捈岎嵗昗偑堦斣巊偄傗偡偄傛偆偱偡丅偙傟傜偺嫵嵽偼捈慄傗墌埲奜偵桳梡惈偑偁傞傛偆偵巚偊偰巇曽偑偁傝傑偣傫丅傓偟傠攠夘曄悢傪偟偭偐傝嫵偊丄捈慄傗墌偵偮偄偰偺懆偊曽偺懡條惈傪嫵偊偨偄婥偑偟傑偡丅
丂椺偊偽丄嶰妏娭悢偺崌惉乮悢嘦乯丄暋慺悢偺嬌宍幃乮悢俛乯丄嬌嵗昗乮悢俠乯偲x=rcos兤丆y=rsin兤傪堄幆偟偨曄宍傪俁夞傕傗偭偰偄傑偡偑丄攠夘曄悢偼悢俠偱妛傇偙偲偵側偭偰偄傞偺偱偡丅
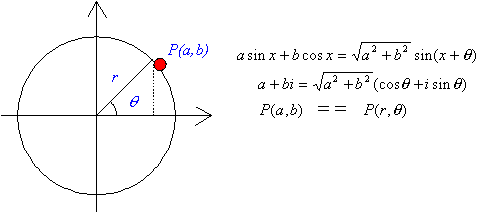
| 椺侾俈丂sin兤+cos兤<1丂傪夝偗丅 |
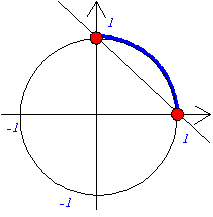
x+y<1丆x2+y2=1傪恾宍偵傛偭偰夝偔偲丄0<兤<兾/2丅
椺侾俉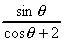 偺嵟戝抣傪媮傔傛丅 偺嵟戝抣傪媮傔傛丅
|
x2+y2=1偲y=k(x+2)偑嫟桳揰傪帩偮偲偒偺孹偒傪峫偊偰丄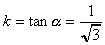
偙偺偲偒丄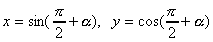
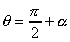
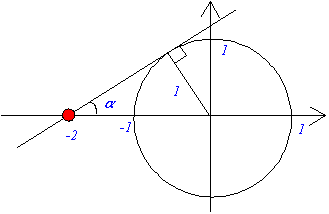
椺侾俋丂x2+y2=1偺帪偵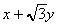 偺嵟戝抣傪媮傔傛丅 偺嵟戝抣傪媮傔傛丅
|
x=cos兤丄y=sin兤偲偍偔偲丄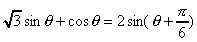
偙偺偲偒丄