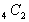条件付き確率について

　確率の試行の独立を数Ⅰで、自称の独立を数Ｂで学習することになっていますが、試行の結果として起こる事柄を事象というのですから、確率の問題の中で試行と事象はほぼ同一に扱われています。このあたりの問題をみてみると、数Ⅰと数Bの問題集には同じ問題が出されていました。また、条件付き確率も場合の数を数え上げてやれば出来る（ただしめんどくさい）のであるから、数ⅠとＢの問題上の区別が付かないように思います。

　授業ではandはかけ算、orは足し算と教えて計算させていますが、生徒は独立と従属をうまく区別しながら問題を解いているようで、条件付きということなど意識しなくても確率の計算は出来ます。

　
例２０（orは足し算の例）
　　次のような道路があるとき、AからDに至る最短経路は何通りか。



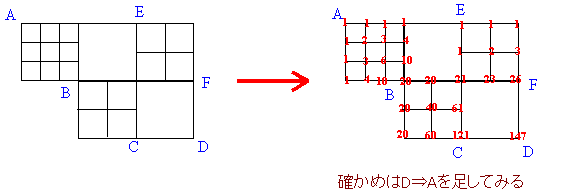
　交差点に行くのは北からいくか、「または」西からあるかであるから足せばよい。

また、確率は順列で、いうのがわたしの解法です。

例２１　袋の中に赤球２個、白球３個ある。同時に２個取り出した時に赤球１個と白球１個を取り出す確率を求めよ。

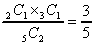
とするのが一般的ですが、人間の目には同時に見えても、実は神様からみるとどちらかは先に出ているから、神様の目から見た確率は　(赤and白)or(白and赤)　といことで

　　
という計算をさせていますが、不都合なく理解しているようです。

例２２　袋の中に赤球５個、白球４個ある。同時に4個取りだしたときに、赤球２個と白球２個を取り出す確率を求めよ。

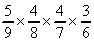
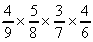
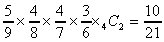
「赤and赤and白and白」or「白and赤and白and赤」…と続きますが、その各々の分数の分母は、９，８，７，６。分母は赤の個数５，４、白の個数４，３であることに注意すると、例えば赤赤白白は、白赤白赤はと同じ答えであるからとなります。
　ここでは赤白の入れ替えの場合です。