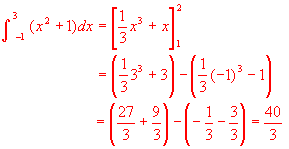
数 学 Ⅱ 《積 分》 No.5 積分の記号
![]()
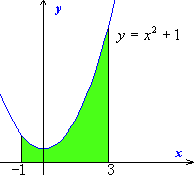
ラクラク積分では、次のように面積を計算しました。
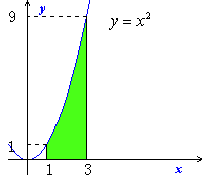
|
この計算を、記号作りの名人と言われたドイツの数学者ライプニッツは次のように書きました。
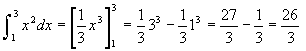 |
記号∫は記号はインテグラルといい、「たす」と言う意味のドイツ語「Summation」の頭文字Sを縦に引き伸ばしたものです。
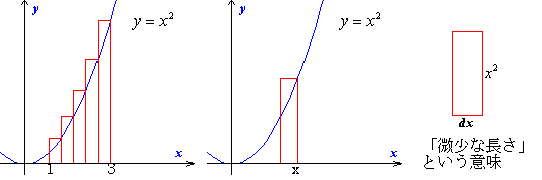
もともと積分とは区分求積法に見られるように、いくつもの長方形に分け、ひとつひとつの面積を計算し、最後にそれらを合計する(細かく分けて、かけて、たす)ことでした。ライプニッツは図のように細かく分けた長方形のうち、あるひとつの長方形の面積を「x2dx」と表し、長方形を端から端(1から3まで)までたすことをインテグラルで表しました。
このように、積分の記号には「細かく分けて、かけて、たす」という積分の歴史的,本質的な意味合いが込められているのです。
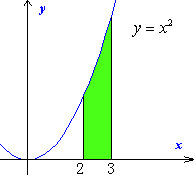
![]() インテグラルで表し、面積を求めてみよう。
インテグラルで表し、面積を求めてみよう。
①
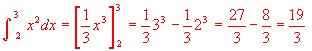
②
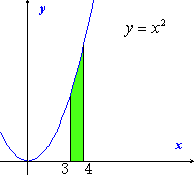
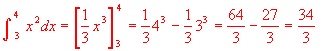
③
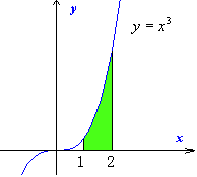
④