以下に示した問題に対する解答例の中には、論理的に不適切な部分があります。それを指摘し（赤ペンで記す）、その理由を、右側余白に簡潔に述べ、正しい解答を求めなさい。

　この解法のほかの解法があれば、別解の欄に記述しなさい。（裏面を利用しても可）

《問題》 0°≦θ＜360°で、次の方程式を解け。

　(1)　sin２θ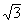＝cosθ　　　　(2)　cosθ−cos２θ＋cos３θ＝１

【解答例】 (1)　sin２θ＝２sinθcosθより 代入して ２sinθcosθ＝cosθ 両辺をcosθ で割って 　２sinθ＝ 　∴　sinθ＝ よって　θ＝60°、120° (2)　cos２θ＝２cos２θ−１ cos３θ＝４cos３θ−３cosθ　より 与式に代入して、cosθ＝ｘとおくと 　ｘ−(２ｘ２−１)＋４ｘ３−３ｘ＝１ ４ｘ３−２ｘ２−２ｘ＝０ 　両辺を２ｘで割って 　２ｘ２−ｘ−１＝０ 　(ｘ−１)(２ｘ＋１)＝０ 　　−１≦ｘ≦１より 　　∴　ｘ＝１、 　　∴　cosθ＝１、 　よって、　θ＝0°、120°、240° 【別解】

cosθで割ることはできない。 理由）　0°≦θ＜360°より -1≦cosθ≦1となるので、cosθ＝０となる場合もある。０となる可能性のあるものでは、割ることができない。その操作をする場合は、cosθ＝０のときと、cosθ≠０の場合に分けて検討する必要がある。 ここでは、この２つの場合に分けずに、一般的な解法を示す。 　２sinθcosθ＝cosθ 　２sinθcosθ−cosθ＝０ 　cosθ(２sinθ−)＝０ 　∴　cosθ＝０，sinθ＝ よって、θ＝60°、90°、120°、270° 　 　(1)同様、ｘ＝０の場合もあるので割ることはできない。よって正しい解答例は、２ｘで因数分解して 　２ｘ(２ｘ２−ｘ−１)＝０ ２ｘ(２ｘ＋１)(ｘ−１)＝０ ∴　ｘ＝０，１， ∴　cosθ＝０，１， よって、θ＝0°､90°､120°､240°､270°