以下に示した問題に対する解答例の中には、不適切な部分があります。それを指摘し(赤ペンで記す)、右側余白に訂正を記しなさい。
この解法のほかの解法があれば、別解の欄に記述しなさい。(裏面を利用しても可)《問題》
kを定数とするとき、xに関する2次方程式
x2-2(k+1)x+(k2+3k-10)=0
の解がすべて正であるkの値の範囲を求めよ。
【解答例】
実数解を持つことより
D/4=(k+1)2+2(k2+3k-10)>0
-(k+7)(k-3)>0
∴(k+7)(k-3)<0
∴-7≦x≦3 …①
また、正の解をα、βとすると、解と係数の関係を用いて
α+β=-2k-1>0
∴ k>-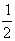 …②
…②
αβ=2(k2+3k-10)>0
k2+3k-10>0
(k+5)(k-2)>0
∴ k<-5、2<k …③
①、②、③より
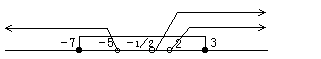
よって 2<k<3
【別解】